| Posted: Nov 03, 2015 |
The complexity of modeling
(Nanowerk News) In recent years, advances in materials synthesis techniques have enabled scientists to produce increasingly complex functional materials with enhanced or novel macroscopic properties. For example, ultra-small core-shell metallic nanoparticles used for catalysis, high entropy alloys made of 6 or 7 elements to give high strength at high temperatures and pharmaceuticals engineered at the nano-scale for more effective drug delivery.
|
|
Modern engineered materials drive progress in many scientific disciplines and are at the heart of next-generation technologies in industrial fields including electronics, energy production and storage, environmental engineering, and biomedicine. As the optical, electronic and mechanical properties of such materials are deeply influenced by atomic structure, solving the structure of engineered materials is of critical importance to unlocking their true potential.
|
|
However, the structures of such materials are often complex and non-periodic at the atomic scale or at the nanoscale. For example, many of the best known thermoelectric materials have structures that are crystallographic on average, but derive their high thermoelectric figure of merit from local atomic distortions. Disordered collections of nanoparticles, on the other hand, have a high degree of short- range order but no long-range order beyond the nanoscale. Additionally, many novel materials are composites, which exhibit complex ordering on multiple length scales, so the complexity faced by the materials scientist wishing to understand the structure of new and novel materials is considerable.
|
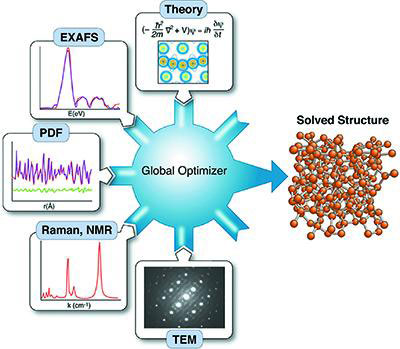 |
| Complex modeling feeds all available data sets and theoretical constraints into a global optimizer to produce a unique structure solution. (Image: S. Billinge et al.)
|
|
The standard techniques of crystallography have proven successful in characterizing a vast array of bulk materials whose atomic structures can be described with crystal models that require only tens or hundreds of parameters. Since X-ray diffraction data typically yield information on hundreds or thousands of diffraction peaks, a unique structure solution can almost always be found for crystalline materials.
|
|
However, for the types of complex materials described above the number of degrees of freedom in suitable structure models is often considerably larger than in the case of a typical crystal. Additionally, complex engineered materials often produce extremely broad peaks in diffraction experiments, due to the fact that they are non-periodic or disordered. Thus, the structure problem is doubly complicated, as diffraction experiments produce less information than corresponding experiments on bulk materials.
|
|
From a standard crystallographic perspective, the structure problem for many complex materials is inherently ill posed, making a unique solution impossible. When the standard techniques of crystallography fail, it is sometimes possible to develop new analytical tools to maximise the information extracted from a diffraction pattern, but even with such advances a unique solution can often not be found to a fundamentally ill-posed problem without defining new constraints or adding additional data.
|
|
To obtain unique structure solutions for complex materials, a new paradigm of analysis is needed: a methodology that can combine different information sources and models into a coherent framework to solve problems using global optimisation. Within this framework, a material with unknown structure could be probed with various experimental tools, such as X-ray diffraction, transmission electron microscopy, small-angle X-ray or neutron scattering, Raman spectroscopy etc. to yield an array of data sets that would then be fed into a global optimiser. Additionally, theoretical inputs, such as density- functional theory could be integrated into the optimisation.
|
|
While each single experimental or theoretical input may not generate enough information to produce a solution, together the pieces of information would regularise the problem, resulting in a unique solution.
|
|
A group of scientists provide a complete description of an implementation of complex modelling, one which is robust, modular and easily adaptable to different types of problems and different combinations of data sets and theoretical inputs ("Complex modeling: a strategy and software program for combining multiple information sources to solve ill posed structure and nanostructure inverse problems"). The key is to break the process down into its constituent parts, which can then be combined and linked as necessary to solve the problem at hand.
|

