| Posted: January 11, 2008 |
Graphene - the indecisive insulator |
|
(Nanowerk News) Graphene, which consists of single sheets of carbon atoms peeled off graphite, has recently been fabricated for the first time. Graphene has unusual electrical properties that originate from the unconventional manner in which its electrons behave. A team from the University of California, the Paul Scherrer Institute in Switzerland and the RIKEN Discovery Research Institute in Wako are gaining insight into graphene by expanding the quantum theory for relativistic particles ("Z2 topological term, the global anomaly, and the two-dimensional symplectic symmetry class of Anderson localization").
|
|
Electron transport in solids is usually non-relativistic and governed by the Schrödinger equation. However the electrons in graphene effectively behave like massless relativistic particles, which are described by a Dirac equation. This means that in two dimensions the electronic energy band is cone-shaped, and gives graphene the potential to switch from a conducting metal to an insulator.
|
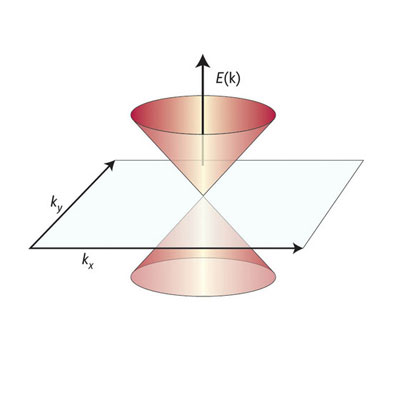 |
| In two dimensions, the electronic energy band in graphene follows a cone-shaped distribution, similar to the behavior of relativistic massless Dirac fermions. (Image: Akira Furusaki)
|
|
“Electrons are scattered randomly by impurities and defects in a solid,” explains project-member Akira Furusaki from RIKEN. “When such scattering happens sufficiently frequently, electrons become localized in a finite region and cannot propagate over a distance. This phenomenon is called Anderson localization.”
|
|
During Anderson localization, the wavefunction—or probability distribution of different states—of an electron is very narrow in space. If all the electrons in a solid are Anderson localized, the solid is an insulator. In contrast, electrons in a conducting metal are free to move, having wavefunctions extended over the entire system.
|
|
Furusaki and co-workers extended an aspect of quantum field theory called the nonlinear sigma model to examine Anderson localizations in graphene. The model is defined whenever electrons move by diffusion, and has been a standard tool to describe transport properties of electrons in disordered solids.
|
|
The researchers discovered that when the nonlinear sigma model is used to describe the transport of two-dimensional Dirac electrons in a random electrostatic potential, a topological term is required in the mathematical formulation (at the same time, a German and Russian team reached a similar conclusion independently ("Quantum Criticality and Minimal Conductivity in Graphene with Long-Range Disorder").
|
|
The topological term arises from Majorana fermions—theoretical particles that are their own antiparticles—originating in the theory of the Anderson localization in graphene. “The presence of a topological term can change low-energy (long-distance) properties of the model drastically and is responsible for metallic transport in graphene,” says Furusaki.
|
|
In future the researchers hope to generalize their theory to three dimensions. “We also plan to examine other systems such as disordered superconductors,” says Furusaki, “in which the transport of low-energy quasiparticles may be highly complex.”
|

