| Posted: January 16, 2009 |
Novel numerical technique permits studying the interaction between elementary particles without approximations |
|
(Nanowerk News) An international team of researchers has developed a numerical modeling technique to study specific types of particles called excitons, which consist of a positively and a negatively charged electron and hole, respectively. The technique includes the influence of a material’s internal structure—the so-called host lattice—without the need to make approximations of any sort ("Exact Treatment of Exciton-Polaron Formation by Diagrammatic Monte Carlo Simulations").
|
|
In an exciton, the electron and the hole are bound together by an electric attraction—known as the Coulomb force – in a fashion very similar to that of an electron and a positron in a hydrogen atom. The presence of the host lattice and its thermal and magnetic excitations that consist of phonons and magnons, respectively—known collectively as the ‘bosonic’ field—can affect the excitons considerably.
|
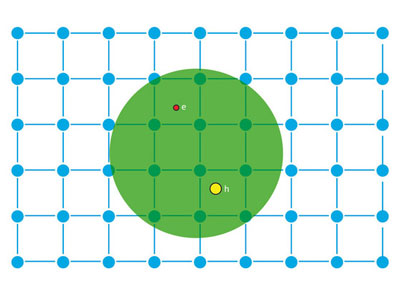 |
| Schematic of an exciton in a host lattice. The electron (red) and the hole (yellow) that constitute the exciton are held together by the Coulomb attraction (represented by the green circle).
|
|
The researchers, including Andrei Mishchenko from the RIKEN Advanced Science Institute in Wako, aimed to develop a technique to study the excitons’ interaction with phonons in an exact way. In particular, they focused on taking into consideration the fact that phonons do not act instantaneously as occurs in the Coulomb attraction. “Previously, the only way to treat the exchange [between electrons and holes] by bosons was an instantaneous approximation, where the influence of particle–boson interaction was included into the model by renormalization of the instantaneous coupling,” explains Mishchenko.
|
|
Mishchenko and colleagues’ technique is known as a Diagrammatic Monte Carlo Method and is based on the diagrams that the Nobel laureate Richard Feynman introduced to quantum field theory. The method per se existed already and was normally used with all variables expressed as a function of spatial coordinates. This, however, limits the size of the area that can be examined in a calculation. The team therefore formulated the algorithm for momentum space. This provides the “possibility to overcome the limitation of the direct space method [for] finite systems and handle the problem [in] a macroscopic system,” says Mishchenko.
|
|
Like any new theoretical method, the team’s numerical technique must be compared with known scenarios to verify its validity, so Mishchenko and colleagues used it to study excitons with different values for the electron and hole masses. They found very good agreement with previous theories within the limit in which it is reasonable to neglect any retardation effect. Importantly however, the results show that in standard conditions it is incorrect to neglect the retardation.
|
|
As Mishchenko explains: “Our ‘free-from-approximations’ results show that the domain of validity of the instantaneous approximation is very limited.”
|

