Logo

A universal law for characteristic temperatures at the nanoscale
(Nanowerk Spotlight) In a previous Spotlight we have reported on a study that has shown that nineteenth century thermodynamics can still provide useful insights into twenty-first century nanosciences; and all this can be done with pencil and paper rather than an expensive super-computer (see: "Nanoscale thermodynamics on the back of an envelope ").
When the size of materials approaches the nanoscale, the surface-to-volume ratio increases and matter begins to behave exotically. Considering this, scientists like Dr. Grégory Guisbiers working at the Institute of Electronics, Microelectronics and Nanotechnology (IEMN) in Northern France can predict size effects on material properties from macroscopic laws, the so-called top-down approach.
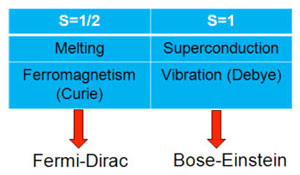
The physical properties of nanostructures have been investigated extensively both theoretically and experimentally. Among these properties, melting temperature, superconductive temperature, Curie temperature and Debye temperature are key physical quantities since they are the characteristic temperatures of melting, superconduction, ferromagnetism and vibration, respectively:
  • The melting temperature is the highest temperature where the solid phase exists under thermodynamical equilibrium.
  • The superconductive temperature is the highest temperature for which the material looses all resistance to the flow of electricity and tend to expel any magnetic fields inside it.
  • The Curie temperature is the highest temperature for which the ferromagnetic phase is stable.
  • The Debye temperature is the temperature corresponding to the maximal energy which can excite lattice vibrations.
    		•
    "It is known that these physical quantities of free-standing nanostructures decrease as the size decreases down to the nanoscale," Guisbiers tells Nanowerk. "The description of different effects observed in nature by only one general equation is the 'Holy Grail' for all physicists. We have achieved this goal for characteristic temperatures through a top-down approach."
    Publishing his findings in an upcoming issue of Physics Letters A ("Universal size/shape-dependent law for characteristic temperatures"), Guisbiers presents a general equation that is based only on the surface area to volume ratio of nanostructures and statistics (Fermi-Dirac or Bose-Einstein) followed by the particles involved in the considered phenomena (melting, ferromagnetism, vibration and superconduction).
    "Experimentally, there exists a relation between all these temperatures. Indeed, the melting temperature is proportional to the Curie temperature, to the square of the Debye temperature and to the square of the superconductive temperature," says Guisbiers. "By shrinking the size of a material, its melting temperature varies as function of its reciprocal size. Therefore, the Curie temperature, the superconductive temperature and the Debye temperature of nanomaterials will be also proportional to its reciprocal size."
    He explains that by analyzing the spin of the particles involved in the four considered phenomena, it will be possible to describe these size effects on four different material properties into only one equation. "Indeed, particles can be distinguished into two groups according the value of their spin. The spin can be seen as the particle rotation around their own axis. Fermions have a half integer spin and are described by a Fermi-Dirac statistic. Bosons have an integer spin and are described by a Bose-Einstein statistic."
    Guisbiers goes on to describe the four different effects he considered for his equation:
  • Melting is a solid-liquid phase transition due to thermal breaking of interatomic bonds and the broken bond results in unpaired electrons characterized each one by a half integer spin.
  • Superconduction is a state where conduction electrons are ordered into pairs of electrons called Cooper pairs of electrons characterized by an integer spin.
  • Ferromagnetism is a net magnetic moment which appears in a material in absence of external magnetic field and is due to partially filled shells of electrons, thus the total spin is uncompensated and characterized by a half integer spin.
  • Vibration is described by phonons (phonon is to vibration what photon is to electromagnetism) which have an integer spin.
    		•
    Here is a table summarizing the spin values of the particles involved in the four considered phenomena:
    spin values of particles
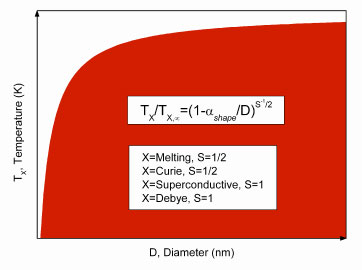
    The general equation is based only on the size of the nanostructure (D), the surface area to volume ratio of nanostructures (αshape∼A/V) and statistics (Fermi-Dirac or Bose-Einstein) followed by the particles involved in the considered phenomena (melting, ferromagnetism, vibration and superconduction). From the distinction between fermions and bosons, this equation indicates the universal behavior of size and shape effects. Furthermore, this equation has no adjustable parameters.
    general equation to describe size and shape effects on characteristic temperatures at the nanoscale
    General equation to describe size and shape effects on characteristic temperatures at the nanoscale.
    This means that the size/shape effect is not only due to the surface area to volume ratio but is linked also to the intrinsic nature of the particles involved in the considered material property.
    Michael Berger By – Michael is author of three books by the Royal Society of Chemistry:
    Nano-Society: Pushing the Boundaries of Technology,
    Nanotechnology: The Future is Tiny, and
    Nanoengineering: The Skills and Tools Making Technology Invisible
    Copyright © Nanowerk LLC

    Become a Spotlight guest author! Join our large and growing group of guest contributors. Have you just published a scientific paper or have other exciting developments to share with the nanotechnology community? Here is how to publish on nanowerk.com.