| Posted: Feb 06, 2017 |
Towards new IT devices with stable and transformable solitons
(Nanowerk News) Unavoidably, each digital information we send around the globe is prone to be lost. Travelling long ways in wires, the initial signal decays and scatters by colliding with impurities and neighboring electromagnetic fields. Therefore, beyond each bit of your desired message, it is necessary to send other hidden bits of information that check for mistakes and take action in case of losses; while devices become smaller and smaller, this issue becomes more significant.
|
|
Scientists at the Center for Artificial Low Dimensional Electronic (CALDES), within the Institute for Basic Science (IBS) are aiming to find innovative ways at achieving a more stable transmission of information. One of their research interests focuses on self-reinforcing solitary wave packets called solitons, which are stable no matter the surroundings.
|
|
In their most recent paper they demonstrated that solitons can be manipulated and outlined how to use them for logical operations. Their experiments and models are published in Nature Physics (" Switching chiral solitons for algebraic operation of topological quaternary digits") and pave the way to a new field of electronics: Solitonics.
|
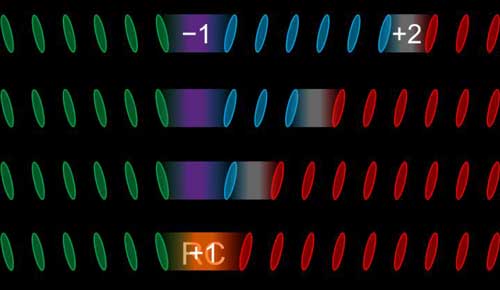 |
| When two solitons meet, they switch type, following a quaternary system made of only four numbers: -1, 0, 1 and 2. In this case a -1 soliton meets with a 2 soliton to form a 1 soliton. (Image: IBS)
|
|
Physicists know that one possible solution to the issue of signal attenuation or noise because of external interferences can come from a mathematical concept called topology. It is related to properties that are not affected by a change in shape. For example, believe it or not, a ball and a pencil are topologically the same, but different from a donut. This is because, with some imagination, you can mold the ball into the shape of the pencil.
|
|
However, when you make a hole in the ball, it becomes a totally different topological object. Holes define the topological state, they can move within the material, but their number does not change even under the presence of pushing and pulling forces.
|
|
A similar concept could be used in IT to protect the flow of information from external interferences and impurities and guarantee its stability over longer distances and time. It sounds like an amazing property but, paradoxically, it is also its own biggest enemy: The transmitted information is too stable, in a way that it is actually too difficult to modify and use. That seemed to be the sad end of the story, until IBS scientists demonstrated a way to manipulate the transmitted signal and possibly apply it to modern electronics.
|
|
One of the key components of the physics of topological system is the soliton, an extremely stable solitary wave packet of energy, which travels though some 1D materials without losing its shape and energy, a bit like a tsunami wave. Scientists began to study topological solitons in the 80's, but were deterred by the seemingly impossibility of manipulating them.
|
|
Last year, IBS scientists explored the properties of solitons on a double chain of indium atoms placed on the top of a silicon surface and they found that solitons could exist in three forms.
|
|
"In a topological sense, it is like having a donut with a lot of holes, where each hole can be of three different shapes corresponding to the three types of solitons," explains YEOM Han Woong, the leading author of this study. "Physicists used to work with solitons (holes) of the same type and the operations you could do with them were limited, but now we have a bigger chance to play with them."
|
|
In this new study, Yeom and his team proved, experimentally, that switching between these solitons is possible. They observed that when two solitons meet, they result in a different soliton, in other words they found that solitons can be transformed, and yet remain immune to the defects of the medium.
|
|
"So far solitons could only be created or destroyed in pairs, no other manipulations were possible, but we showed that these solitons can be switched from one to another, and even used for logical operations", continues Yeom.
|
|
These three types of solitons can also be represented by digits (1, -1 and 2) and the condition without solitons as zero (0), creating a quaternary mathematical system. The four digits can then be used for mathematical computations.
|
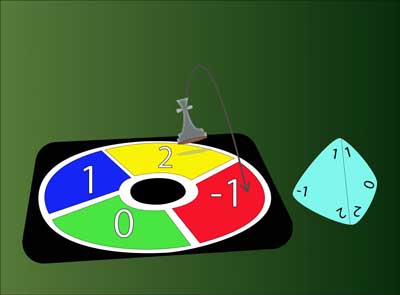 |
| While the binary code used in our current computers is made of 0s and 1s. A quaternary system, like the one proposed by IBS scientists, consists of four digits (0, 1, 2 and -1) and would allow more operations. The researchers modeled solitons addiction. For example, a soliton represented by the number 2, and another one represented by the number 1 can be added to form a new soliton (n. -1). Indeed, in this 4-base system, 2+1 makes -1, and it is easy to understand why if you imagine a small and circular "game of the goose" where you move clockwise (or anticlockwise) depending on the number you get by rolling a four-sided die containing the numbers 0, 1, 2 and -1. If you are in the box n. 2 and you get n. 1 on the dice, you are going to reach the -1 square. (Image: IBS)
|
|
Quaternary digit systems, and multidigit systems in general, have several advantages over the binary (0, 1) system that we are currently using. They allow more operations and information storage in less space and they could bring us a step closer to brain-like devices, which mimic the way information is computed and stored by our neuronal circuits.
|
|
Opening a new field of electronics, dubbed solitonics, IBS scientists imagine new generation IT devices that combine silicon and solitons. "We are using solitons travelling in indium atoms on a silicon surface, and we imagine that this structure that could be implemented in current silicon devices, creating hybrid systems," explains KIM Tae-Hwan, first author of this study.
|


