| Posted: Nov 07, 2017 |
A new concept for a unidirectional waveguide
(Nanowerk News) In the past decade, a new type of material has attracted raising attraction: the so-called topological insulator. This class of materials exhibits a very peculiar property: they behave like insulators in the interior, but contain conducting states at their boundaries. As these states are “topologically” protected, the states are very robust against imperfections, and electric currents can flow almost without any dissipation. This makes these materials extremely interesting for the task of quantum communication and quantum computing, for example.
|
|
Now Dr. Tao Shi (at present Chinese Academy of Sciences, Beijing) and Prof. Ignacio Cirac from the Max Planck Institute of Quantum Optics in Garching, together with Prof. Jeff Kimble from the California Institute of Technology (Pasadena, USA), have developed a detailed scheme for an experimental setup to realize a 2-dimensional topological insulator with classical optical networks (PNAS, "Topological phenomena in classical optical networks").
|
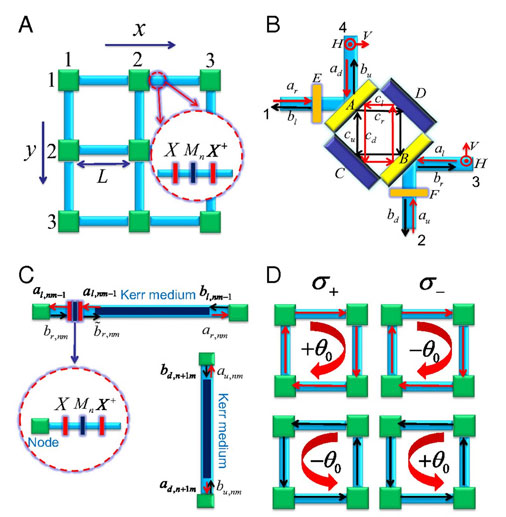 |
| Scheme of the optical nework. (© PNAS)
|
|
“In this network, photon modes play the role of the electronic states in a solid state layer,” explains Dr. Tao Shi. “By preparing chiral photon modes at the boundary, we may be able to build a one-way electromagnetic waveguide, in which light can only propagate in one direction, while the opposite direction is prohibited.“
|
|
Solid state crystals are characterized by their band structure. In case of an insulator, the so-called valence band, in which all electronic states are occupied, is separated from the conduction band by a large forbidden zone. This, however, only holds for infinite samples.
|
|
In case of a confined crystal or layer, the electronic states at the surface or edge, respectively, differ from those in the interior, and sometimes they emerge in the middle of the forbidden zone. As the shape of the band structure is mathematically described by a certain topological number, these systems are called in short “topological insulators”.
|
|
The chirality of the edge states is locked to the spin of the electron, and is consequently protected by time-reversal symmetry: a reverse in direction would imply a flip of the spin direction. For a certain class of materials with a “nontrivial” topological number this is not allowed. Therefore, the states are protected and robust against imperfections or deformations, as long as the perturbations are small.
|
|
In a certain class of electronic 2-dimensional topological insulators also the so-called quantum spin Hall (QSH) effect can be observed. Intuitively, this effect describes the phenomenon that electrons with different spins are subjected to oppositely directed magnetic fields.
|
|
Different from previous schemes, the scientists propose a setup made of optical passive elements such as fibres, beam splitters, and wave plates, whereby system losses are reduced to a large extent. By constructing the nodes of the network with a “bad” cavity, i.e. a cavity with high damping, they are able to dramatically enhance the topological bandgap to the scale of the free spectral range. As a consequence, the edge modes survive in the larger frequency domain with much longer lifetime. Furthermore, the interplay between the topology and the Kerr non-linearity induces the generation of squeezed edge modes.
|
|
“The optical analogue of a topological insulator paves the way towards building the one-way wave guide,” Dr. Shi points out. “Apart from that – our ultimate goal is to realize the fractional quantum Hall effect (FQHE) in this photonic system. To this end, we have to induce strong photon-photon interactions by means of atoms. We would also like to see some exotic topological phases in the photonic system, which can be very different from those observed in conventional condensed matter systems.“
|

