| Posted: Apr 19, 2018 |
Graphene changes elastic properties depending on applied force
(Nanowerk News) A group of scientists, including specialists from Landau Institute for Theoretical Physics (ITF), described a universal characteristic, in which many unique graphene properties are "hidden". It turned out that abnormal graphene behavior can be fully characterised by Poisson ratio, which determines material capability to shrink or extend in transverse dimension. Moreover,scientists found key factors that can influence this characteristic. The results are published in Physical Review B ("Stress-controlled Poisson ratio of a crystalline membrane: Application to graphene").
|
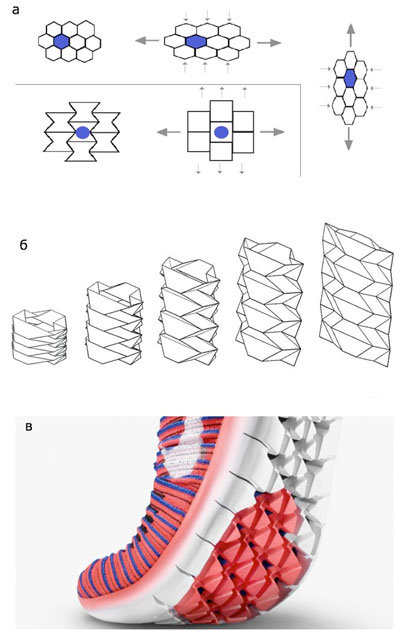 |
| a) Folded elements of auxetic materials straighten out, increasing its transverse dimension under stretching. b) Products made of any materials, folded according to the rules of the miura-ori: a folding system, which makes it possible to straighten the construction in one movement, also possess auxetic properties. c) Sneakers sole made up of overlapping triangles behaves like an auxetic under pressure. (Image: Article authors)
|
|
Graphene is a two-dimensional sheet consisting of one layer of carbon atoms. Due to its unusual properties, today graphene is considered one of the most promising materials for new non-silicon elastic electronics. One of the most interesting things about graphene is the relation between its unique elastic and electrical properties. For instance, graphene shows extremely high mobility of electric charges, which can change drastically under elastic stress. Physicists tried to find a universal physical characteristic fully reflecting this unusual behaviour. This would make it possible to use graphene more effectively, as well as create new materials with required exotic properties. However, until recently researchers could not find any such parameter.
|
|
The key to understanding this question lied in the unusual behavior of graphene under stretching. Most common materials shrink in transverse direction while stretching: a rubber band is a typical example. However, about a hundred years ago, the German physicist Voldemar Voight discovered that pyrite crystals, on the contrary, extend under stretching. Such materials were called auxetics, and in the late 1970s scientists obtained first artificial auxetic. The secret of such materials comes from their unusual geometry. Although in a relaxed state auxetic structural elements are folded, when stretching is applied they unfold and grow in size.
|
|
Auxetics have a number of unusual features that will help improve existing technologies and create new ones. "Conventional materials expand when heated and this impairs their original properties through various mechanical stresses and disturbances. Auxetics can, on the contrary, shrink. So there is an idea to create combined materials with zero expansion ratio using auxetics. As the temperature rises, the conventional compound of such materials will tend to expand, but auxetic compound will compensate for this," comments Valentin Kachorovskii, a leading researcher at The Ioffe Institute and ITF.
|
|
The feature determining material capability to shrink or extend in transverse dimension under tension is called the Poisson ratio. In auxetics it is negative, in ordinary materials -- positive. "Scientists were long interested in graphene Poisson ratio," says Kachorovskii. "For a long time we thought that it was equal to the universal negative value -?. However, a number of recent numerical calculations showed that graphene Poisson ratio could be both positive and negative. At first glance, results of various calculations contradict each other completely."
|
|
Direct experimental verification of this parameter is difficult. Graphene is hard to obtain in isolation: it is usually "grown" on various substrates, and their characteristics mask the true value of graphene Poisson ratio. What is more, samples of isolated graphene are so small that it is practically impossible to attach brackets for controlled stretching. At the same time, researchers and engineers who develop new carbon-based technologies need to know exactly whether graphene is auxetic or not.
|
|
Authors of the new work managed to "reconcile" contradictory results of previous calculations and find parameters that exactly determine the Poisson ratio of graphene. Physicists found out that it is a variable value depending on tensile force applied. "With a very large force, graphene behaves like a normal material, demonstrating positive Poisson ratio. However, when the applied force decreases, we find ourselves in an area where graphene exhibits typically auxetic properties," notes Kachorovskii.
|
|
Scientists explained this unusual link between Poisson ratio and stretching. On popular images graphene is shown as a two-dimensional sheet of carbon atoms, usually flat. However, in reality so-called bending waves run along this "sheet". They tend to turn graphene from a flat state into a crumpled state. "This is called a crumpling transition," Kachorovskii explains.
|
|
"For a long time the theory of membranes predicted that due to this phenomenon two-dimensional crystals such as graphene could not exist in principle. They would always strive to shrink into a ball. As we see, this assumption was a mistake since along the surface of graphene ordinary compression-extension waves run along with bending ones. Nonlinear interaction between two wave types does not allow the membrane to shrink into a ball. Even though, the dimension of such crystals does not actually equal to two. Due to crumpling transition, it is in an intermediate state between two and three dimensions."
|
|
Membrane striving to curl due to ordinary compression-extension waves competes with the effect of smoothing transverse waves due to an external applied force. This results in a changing sign of Poisson ratio. In other words, if the external force is high, the abnormal auxetic properties are suppressed and Poisson ratio is positive. As the scientists showed, the unusual properties of graphene are based on that slightly crumpled resting state.
|
|
"In folds of transverse bending waves additional energy is stored, which accounts for graphene abnormal elasticity and other unusual properties. For example, when heated graphene begins to shrink in the longitudinal direction, since the entire extension goes to transverse folds," continues Kachorovskii. "And universal characteristic which determines exactly graphene behavior is Poisson ratio. With its help, you can describe and predict a large number of properties of graphene and other materials."
|
|
What is more, current work contains explanation why previous studies of the Poisson ratio of graphene had contradictory results. "We derived an analytically complete system of equations for the elastic balance of graphene sheet. It turns out that there are two modes of behavior for graphene membrane. In the usual one, all the properties of graphene are determined by standard formulas and Poisson ratio is positive. At the same time, for samples larger than so-called Ginzburg length, an abnormal elasticity regime is realized, leading to negative Poisson ratio", adds Kachorovskii. For graphene, Ginzburg's length ranges from 40 to 70 angstroms. The size of samples used in practice is certainly greater, therefore it is possible to see the most unusual auxetic behavior.
|
|
The explanation of this phenomenon is also connected with waves of different types, which interact with each other in a very complicated manner. "Ginzburg length characterizes the scale at which these interactions can no longer be neglected as they begin to abnormally shift the material. For example, such large-scale interaction does not allow two-dimensional crystals to shrink into a ball", explains Kachorovskii. Different substances have different Ginzburg lengths and knowing them is extremely important for the development of new materials.
|
|
"Often people create new materials without calculating Ginzburg length and then they try to find something unusual in their properties. But our work shows that if Ginzburg length is as large as 1 kilometer, for example, regular sized samples will not show any special properties", Kachorovskii notes.
|
|
The fact that graphene can stretch normally or abnormally depending on the applied force in perspective will help create hypersensitive sound sensors, for example.
|
|
"Sound waves stretch graphene membrane, and depending on the degree of stretching graphene noticeably changes the electrical resistance. Calculations show that sensitivity of such detector can be gigantic. In addition, in auxetics the sound velocity is noticeably higher than in "normal" materials. The value of other elastic constants, for example, the Young's modulus remains the same. Therefore, when graphene becomes stretched to the state of auxetic, the sound in it spreads very quickly. This allows us to create ultra-fast sensors which can detect a very rapid change of oscillations", summarizes Kachorovskii.
|

