| Apr 26, 2019 | |
Mikado inside a nano box: Bertrand's paradox revisited(Nanowerk News) When you shake a box filled with Mikado sticks, will you get a uniform spreading of the sticks inside the box? This question touches Bertrand’s paradox, a classic in mathematics. In 2D, this is already an intriguing question, so what if you move to 3D? And, to make it more complex, what if you want to know how big the holes are between the sticks – ‘chords’ in mathematics. |
|
| For designing nano mikado boxes for photonics purposes, scientists of the University of Twente wanted to be able to determine the free space between the sticks. They now come up with a method using tiny moveable balls blowing up. This method is published in Physical Review E ("Uniform line fillings"). | |
| The fact that a classic 19th century paradox is revisited for designing innovative nanostructures, is remarkable. The paradox, by Joseph Bertrand, is about chords, the lines you can draw between two points on a circle. If you take an equilateral triangle, draw a circle around it, what will be the of drawing chords that are bigger than the trial’s lengths. | |
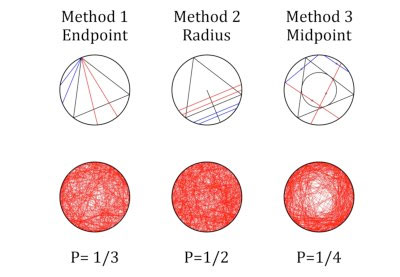
| Bertrand described three different methods that give three different answers. It seemed clear that the way you start shaping the chords, is important. Many years later, Edwin Thompson Jaynes broke the paradox. He stated that there is only one of three methods, capable of filling the circle with chords in a homogeneous way. In this way, the center part of the circle is not more transparent than the edges. | |
 |
|
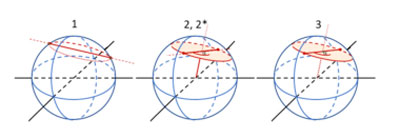
| Three methods, three outcomes in Bertrand's paradox. Draw a random line from one point on the circle to another (1), choose a random radius and angle and draw a line perpendicular to it (2), or choose a random point inside the circle and consider this as the midpoint of a line (3). Only the second method gives a uniform density. Below: from 2D to 3D. (Image: University of Twente) | |
 |
|
Blowing bubbles |
|
| For determining the optical properties of new materials, Pepijn Pinkse and his colleagues wanted to know the size of the holes in between the chords. This says something about the transparency of a new nanostructure. The researchers therefore developed a methode using an infinite number of tiny bubbles that are blown up slowly. They move the bubbles, so they can keep on growing without being 'cut through' by a chord. At the moment no further growth is possible, the size of the hole is known. And you also know if the holes are spread in a homogenous way. | |
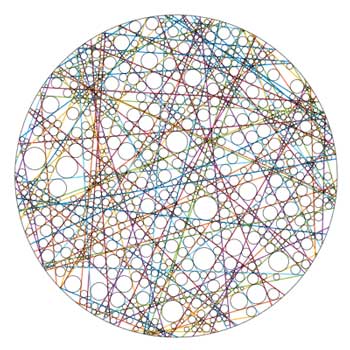 |
|
| For new nano mikado boxes, this method gives new ways of calculating the materials properties like transparency for certain wavelengths. The results are also important in determining the dose of radiation in, for example, X-Rays. Here, you want to now the average length of the rays crossing a certain volume. | |
| Research has been done by the Complex Photonic Systems group, part of the MESA+ Institute of the University of Twente. |
| Source: University of Twente | |
|
Subscribe to a free copy of one of our daily Nanowerk Newsletter Email Digests with a compilation of all of the day's news. |
