| Dec 14, 2021 |
Losing isn't always bad: Gaining topology from loss
(Nanowerk News) Losing particles can lead to positive, robust effects.
|
|
An international collaboration has demonstrated a novel topology arising from losses in hybrid light-matter particles, introducing a new avenue to induce the highly-prized effects inherent to conventional topological materials, which can potentially revolutionise electronics.
|
|
Led by Singapore’s Nanyang Technological University (NTU) and the Australian National University (ANU), the study represents the first experimental observation of a non-Hermitian topological invariant in a semiconductor in the strong light-matter coupling regime supporting formation of exciton-polaritons.
|
Losing is not always losing
|
|
Losses, such as friction or electrical resistance, are ubiquitous in nature, but are seen as detrimental to devices.
|
|
In electronics, for example, resistance leads to heating and limits computing efficiency.
|
|
In photonic systems, photons easily escape confinement, limiting transmission efficiency.
|
|
“However, this negative view about loss has significantly changed recently, thanks to advances in non-Hermitian physics, which have shown that losses can lead to striking effects not possible in a ‘perfect’ lossless world,” says Prof Elena Ostrovskaya from the Australian National University.
|
|
Non-Hermitian physics directly incorporates losses and/or gain into quantum mechanics.
|
|
Taking advantage of analogy between quantum mechanics and classical wave physics, recent advances in photonics demonstrated that judicious control of losses can lead to counter-intuitive effects, such as lasers that turn on despite increasing loss, robust switching between lasing modes, and irreversible propagation of light.
|
|
Studies of non-Hermitian effects in quantum condensed matter systems, such as electronic materials, are less common.
|
Gaining topology from loss
|
|
Losses can induce nontrivial topology, turning a conventional material into a topological one.
|
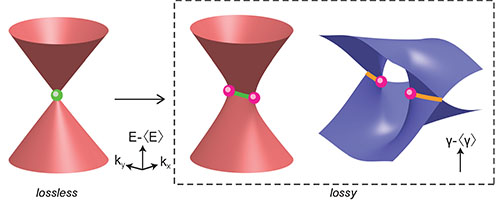 |
| Band structure in the lossless (real-valued) and lossy (left, real part; right, imaginary part) cases. The conical intersection (green dot) in the lossless limit transforms into a pair of exceptional points (pink dots) when a particular type of loss is added. (Image: FLEET)
|
|
Topological electronic materials are classified using topological invariants (eg, the Chern number), a number that quantifies how the electron wavefunctions effectively wind or rotate in momentum space.
|
|
Materials with the same topological invariant have the same topology.
|
|
If two materials with contrasting topology are merged, robust effects, such as dissipationless one-way transport, occurs at their interface.
|
|
Electrical conduction along such dissipationless pathways, without the scattering that causes dissipation of energy and heat in conventional materials, allowing electrical current to flow with almost zero wasted dissipation of energy.
|
|
In this study, the team mixed excitons (electronic excitations) in lead-halide perovskite semiconductor with photons to create exciton-polaritons.
|
|
“Typically, one needs exotic materials or sophisticated material engineering to induce topological behaviour. However, in this work, we discovered that the mere presence of loss in an exciton-polariton system based on lead-halide perovskite causes it to exhibit a nontrivial topology”, says Dr Eli Estrecho (ANU), one of the lead authors of the paper (Science Advances, "Direct Measurement of Non-Hermitian Topological Invariant in a Hybrid Light-Matter System").
|
|
The team carefully measured the energy and linewidths at different momenta and polarisations of polaritons in the system.
|
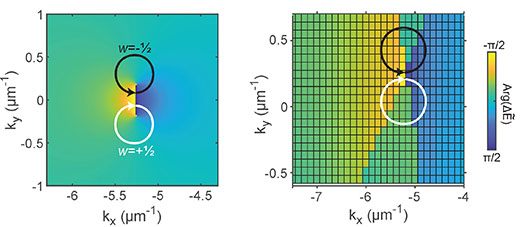 |
| Theoretically predicted (left) and experimentally measured (right) winding of the difference of the complex bands (the non-Hermitian topological invariant) around the pair of exceptional points. (Image: FLEET)
|
|
The energy and linewidths correspond to the real and imaginary parts of the complex energy of the lossy system in the language of non-Hermitian physics. And the two polarisation states give rise to two distinct energy bands in momentum space.
|
|
From this analysis, the team found the points where both real and imaginary parts of the two complex energy bands coincide. These are called exceptional points, and in this system they occur in pairs.
|
|
This would not have been possible if the linewidths were neglected, as was typically done in previous works.
|
|
Furthermore, the team found that the complex energies rotate with a defined handedness and phase around the exceptional points. In fact, the phase winds exactly by as predicted by theory – this quantity is the new topological invariant that arises only in non-Hermitian systems.
|
|
“This is the first direct measurement of a non-Hermitian topological invariant associated with an exceptional point in momentum space of a condensed matter system,” says Dr Rui Su (Nanyang Technological University), one of the lead authors from study.
|
|
Furthermore, the team found that the winding of the wavefunctions and the energy bands are distinct from each other, confirming that they indeed observe a novel topology.
|
|
This work introduces a new avenue in designing topological materials, complementing conventional topology. Instead of avoiding loss, losses can be re-engineered or introduced intentionally to induce topological effects in an inherently non-topological system.
|
|
This could be instrumental in exploiting robust effects due to topology towards realizing a topological transistor in a lossy system.
|
|
Furthermore, because exciton-polaritons in perovskites can exhibit collective quantum behaviour – a Bose-Einstein condensate, this work paves the way for studying non-Hermitian topological effects on the quantum behaviour of condensates and superfluids.
|
Expanded focus from parameter to momentum space
|
|
The ANU group has previously used polaritons to observe non-Hermitian degeneracies called exceptional points and have shown chiral flow of polaritons due to these points.
|
|
However, these points were observed in parameter space.
|
|
This time around, the exceptional points are demonstrated in momentum space, which can directly affect the propagation of the particles, including polariton superfluids.
|
|
“Creating these exceptional points in momentum space paves the way towards studies of combined effects of topology and non-Hermitian physics in exciton-polariton systems,” says Dr Eli Estrecho.
|


