| Jun 08, 2023 |
Topological phase protection reams to sub-symmetry
(Nanowerk News) An international team led by researchers at Nankai University in China and at University of Zagreb in Croatia, along with team at the Institut national de la recherche scientifique (INRS) in Canada, led by Roberto Morandotti has made an important breakthrough in the study of topological phases.
|
|
Their findings were recently published in Nature Physics ("Sub-symmetry-protected topological states").
|
|
In the last decade, topological photonics has attracted increasing attention due to the unique prospects to achieve light manipulation with high performance in terms of robustness and stability. Discoveries in topological photonics have opened the way to the development of a novel generation of photonic devices, such as topological lasers and cavities, featuring topologically protected states that are immune to disorders and defects.
|
|
The concept of topology in physics is inherited from mathematics, where topology is employed to study geometric properties of an object concerning quantities that are preserved under continuous deformation. Two objects are topologically identical when the surface of one can be continuously deformed into that of the other one and vice versa, e.g., a coffee cup and a torus are equivalent from a topology viewpoint.
|
|
In physics, the concept of topology is employed to describe the energy band characteristics, leading to prediction of novel topological states of matter and various topological materials. Different topological phases (trivial and nontrivial) are distinguished by appropriately introducing quantized topological invariants, which enable establishing a link between the bulk properties and the emergence of the feature at the boundary of these materials, known as the “bulk-boundary correspondence”. In this regard, the most distinctive feature of a nontrivial topology is the existence of robust topological boundary states protected by specific spatial and/or intrinsic symmetries.
|
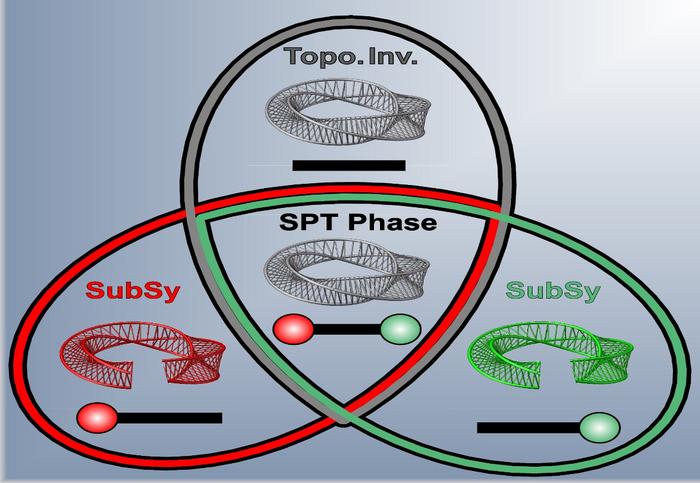 |
| Schematic illustration classifying perturbations in the symmetry-protected topological phase (SPT phase). The overlapping region surrounded by red, gray, and green lines represents a symmetry-protected topological phase featuring topological invariant and corresponding topological boundary states. The gray line is a set of perturbations affecting the boundary states but not breaking the topological invariant of the overall system. Red and green line areas show boundary states protected by their respectively associated sub-symmetry. Illustrated example shows two sets of perturbations that satisfy the sub-symmetry but destroy the topological invariant of the overall system. In this case, sub-symmetry protects boundary states. (Image: Domenico Bongiovanni and co-authors)
|
|
In general, in systems of symmetry-protected topological phase (SPT phase), it is believed that the close relationship between topological boundary states, topological invariants, and one or more overall symmetries is indispensable for maintaining topological protection against perturbations. As consequence, both topological invariants and topological boundary states are irretrievably affected by any distortion that breaks the underlying symmetry.
|
|
In this work, the international research team has challenged this traditional common belief, and thus broaden the understanding of SPT boundary states. They found that even if the system no longer has quantized topological invariants and some kinds of global symmetry, the topological boundary states can still exist in the corresponding subspaces, protected by the so-called “sub-symmetries”.
|
|
“Our discovery challenges the common thinking of the symmetry-protected topological phase in topology and renews the correspondence of topological invariant and boundary states”, said Domenico Bongiovanni one of the main investigators, Postdoctoral researcher at INRS-EMT. “Our idea has the potential to explain the topological origin of many unconventional states and can find application in different platforms and physical systems.”
|
|
The researchers, by introducing and exploring the concept of sub-symmetry, found that global symmetry in the traditional sense is not completely necessary for the protection of topological boundary states. In this regard, topological boundary states are preserved as long as the symmetries of specific subspaces are satisfied, even when the overall topological invariants no longer exist.
|
|
The research team cleverly designed and fabricated photonic lattice structures using a cw-laser writing technique to meet the conditions of different subspace symmetries. The experiments demonstrated a proof of concept with two most typical topological lattices: one-dimensional SSH and two-dimensional Kagome lattices.
|
|
In addition, the team innovatively introduced the concept of long-range coupling symmetry into the Kagome lattice model, which resolves the current controversies about the existence and topological protection of higher-order topological states in the Kagome lattice.
|
|
This study not only challenges the traditional comprehension of topological states protected by symmetry but also provides new ideas for the research and application of topological states in different physical backgrounds. This impact of this work is expected to further promote the development of topological photonics and its cutting-edge interdisciplinary fields, as well as the research and development of a new generation of topological photonic devices based on sub-symmetry-protected boundary states.
|

