| Sep 22, 2014 |
Where is that spacecraft?
|
|
(Nanowerk News) Space surveillance is inherently challenging when compared to other tracking environments due to various reasons, not least of which is the long time gap between surveillance updates. “Unlike the air and missile defense environments where objects are frequently observed, the space surveillance environment data is starved, with many objects going several orbital periods between observations,” according to researcher Joshua Horwood. “Thus, it is more challenging to predict the future location of these sparsely-seen objects and they have a tendency to get lost using traditional methods. A new way of tracking them, the Gauss von Mises (GVM) distribution, has improved predictive capabilities that permit one to more effectively maintain custody of infrequently-observed space objects.”
|
|
In a paper published in July in the SIAM/ASA Journal on Uncertainty Quantification ("Gauss von Mises Distribution for Improved Uncertainty Realism in Space Situational Awareness"), authors Horwood and Aubrey Poore, both of Numerica Corporation, propose a more statistically rigorous treatment of uncertainty in the near-Earth space environment than currently available. The method proposed uses a new class of multivariate probability density functions, called the Gauss von Mises (GVM) family of distributions.
|
|
“By more faithfully representing the uncertainty in a space object’s orbit, the GVM distribution allows one to more accurately predict the future locations of satellites and debris,” says Horwood. “Uncertainty propagation using the GVM distribution can be achieved at a computational cost commensurate with traditional methods and can maintain a proper characterization of the uncertainty for up to eight times as long.”
|
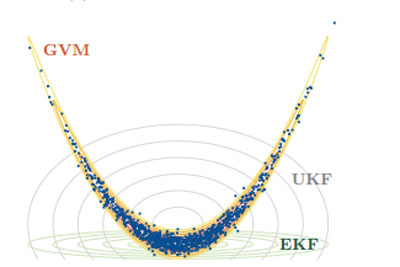 |
| The uncertainty of a space object’s orbital state at different epochs computed from the prediction steps of the traditional extended Kalman filter (EKF), unscented Kalman filter (UKF), and Gauss von Mises (GVM) filter, and a particle filter. Shown are the respective level curves in the plane of the semimajor axis and mean longitude coordinates. The GVM distribution correctly characterizes the uncertainty as depicted by the particle ensemble. (Figure courtesy of Numerica Corporation)
|
|
The uncertainty of a space object’s orbital state at different epochs computed from the prediction steps of the traditional extended Kalman filter (EKF), unscented Kalman filter (UKF), and Gauss von Mises (GVM) filter, and a particle filter. Shown are the respective level curves in the plane of the semimajor axis and mean longitude coordinates. The GVM distribution correctly characterizes the uncertainty as depicted by the particle ensemble. Figure courtesy of Numerica Corporation.
|
|
It is important to study uncertainty in the space surveillance tracking environment in order to protect space assets and maintain awareness of potentially adversarial space deployments. The proper characterization of uncertainty enables us to allocate resources in order to gain as much information about the system as possible, and detect satellite maneuvers. Better uncertainty quantification also helps us track and look for close approaches between any two space objects, a process called conjunction analysis.
|
|
Horwood explains further with an example, “In the problem of conjunction analysis, the use of the GVM distribution can provide a more reliable probability of collision and allows conjunction assessments further into the future. This translates into fewer false alarms and hence fewer expensive maneuver operations that have to be performed on operational spacecraft.”
|
|
In order to quantify uncertainty, proper characterization of a space object’s full state probability density function (PDF) is required to faithfully represent the statistical errors. The GVM distribution approach is supported by a suite of next-generation algorithms for uncertainty propagation, data association, space catalog maintenance, and other space situational awareness functions. What distinguishes the GVM distribution is that it is defined on a cylindrical manifold, and such coordinates, used in conjunction with the GVM distribution, can provide a statistically rigorous treatment of uncertainty needed for orbit determination and tracking.
|
|
Methods proposed in this paper will be beneficial for studying various aspects of future space surveillance. “A quantification of the uncertainties in space surveillance is a prerequisite for robustly tracking hundreds of thousands of space objects that are expected in the future,” says Horwood. “This involves various levels of research including sensor-level processing (to improve the characteristics of the measurement errors and biases), propagation of uncertainty, dynamics and space environment modeling, inverse problems such as statistical orbit determination, and high performance computing to serve the growing space catalog.”
|

