| Posted: Jun 01, 2012 | |
Summary of time reversal symmetry in optics |
|
| (Nanowerk Spotlight) New research explores the uses of time reversal symmetry in optics, with a focus on quantum optics. "Time reversal symmetry in optics" in Physica Scripta is authored by Gerd Leuchs and Markus Sondermann, both affiliated with the University of Erlangen-Nuremberg and the Max Planck Institute for the Science of Light in Erlangen, Germany. The article compares time reversal with optical phase conjugation, and illustrates the concept of time reversal symmetry with several examples in classical and quantum optics. | |
| Time reversal symmetry is the physical property that events can occur in a forward or backward direction through time, with no fundamental distinction due to the direction. Time reversal symmetry applies to both classical and quantum optics, as well as areas of physics outside of optics. The authors note that the property holds true in all areas of physics, with possible exceptions only under rare conditions in particle physics. | |
| The counterintuitive notion of time reversal symmetry appears to violate everyday expectations. Many ordinary events, such as fluids spilling or people speaking, go through time in one direction and seem impossible in reverse. Nonetheless, ordinary events also obey time reversal symmetry laws. The apparent impossibility of time reversal comes from the massive number of intricately connected parts, such as droplets of spilling fluids, which make the probability of "reverse spilling" vanishingly small. The event can still proceed identically whether going forward or backward through time, however the forward direction dominates statistically. Physically, forward and reverse motion through time operate almost identically. Intuitively, forward and reverse motion through time operate almost oppositely. | |
| In optics, whether classical or quantum, physical laws correspond with time reversal symmetry. Explanations apply to optical phenomena equally well regardless of direction through time. The authors use this property to optimize problems in pedagogical and modern optics. Examples include photonic absorption, photonic storage and retrieval, electromagnetic focusing, and fluorescence microscopy. | |
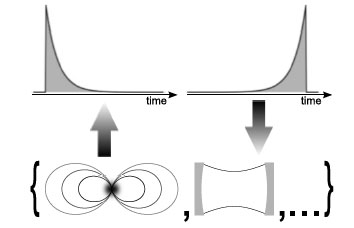 |
|
| Paradigmatic systems involving exponentially decaying optical field amplitudes: spontaneous emission from a two-level atom with an electric dipole transition and field amplitude inside an empty optical resonator. (© IOP Publishing) | |
| Time reversal symmetry relates to optics through phase conjugation. The phase conjugation of a wave reverses the propagation properties of the wave. For a wave that progresses forward through time, phase conjugation sets the wave backward to a state from which its forward progress by the same amount returns the wave to its initial state. | |
| To analyze a system with time reversal symmetry, the system substitutes a time of the same amount but opposite direction. Over an electric field broken into its spectral components, time reversal substitutes elapsed time with its opposite, the same amount of time before the initial state of the field, resulting in the complex conjugation of all spectral amplitudes. Conjugating an electromagnetic wave with exponentially decreasing amplitude results in a wave with exponentially increasing amplitude, a time reversal. Conjugating a monochromatic, outwardly moving spherical wave results in an inwardly moving reversal of the wave. | |
| The authors emphasize that "time reversal is equivalent to inversion of motion in all degrees of freedom". Time reversal, or phase conjugation, reveals optimal amplitude distributions for simple cases like the illustrations cited, and the method also has practical applications. | |
| As an optical system that appears not to have time reversal symmetry, the authors describe an optical isolator. An optical isolator combines two polarizers with a Faraday rotator to rotate the polarization of an electric field. The rotation appears asymmetric through time, unless also accounting for the current flow and magnetic field of the Faraday rotator. | |
| In quantum optics, time reversal symmetry applies to the absorption in free space by a single atom of a single photon, as an example. Absorption contrasts with spontaneous emission, with either process going optimally as the exact opposite of the other. Theoretically, an absorbed wave moving inward toward an atom could match an emitted outward moving wave packet with properties reversed in time. However, perfect time reversal would require an infinitely precise temporal and spatial input. Therefore optical devices can optimize focus at close to, but not exactly, 100% absorption. An additional constraint comes from the atomic momentum which is entangled with the photon. | |
| One approach to time reversal of the interactions between atom and photon directly phase conjugates the spontaneously emitted photon. Beyond the difficult technical challenges, quantum uncertainty limits phase conjugation. A technical challenge applicable to classical optics results from long light pulses, of around one meter, which exceed the size of phase conjugating materials. More fundamentally, phase conjugation adds vacuum noise as with optical amplifiers. The noise prevents pure phase conjugation, and thus quantum time reversal symmetry. However, the authors note that practical uses of time reversal symmetry present themselves for optics. | |
| By Frank Smith. Frank Smith writes about science and technology, with a focus on light. | |
|
Become a Spotlight guest author! Join our large and growing group of guest contributors. Have you just published a scientific paper or have other exciting developments to share with the nanotechnology community? Here is how to publish on nanowerk.com. |
|
