| Aug 16, 2022 | |
In-memory mathematical operations with spin-orbit torque devices |
|
| (Nanowerk Spotlight) Analogue arithmetic operations are the most fundamental mathematical operations used in image processing, signal processing and artificial intelligence (AI). Under error-tolerant circumstance, compared to the digital processor, analogue computing presents a promising and possibly revolutionary paradigm in recent years, as it doesn’t need analogue-to-digital conversion and can allow massively parallel operation. | |
| Meanwhile, in-memory computing offers high performance and energy-efficient computing paradigm. Therefore, it is crucial to explore in-memory analogue computing (IMAC), offering an attractive solution to the energy consumption and area issues. | |
| At present, IMAC based on non-volatile memory array is mainly applied to realize multiplication-accumulation computing (MAC). However, in this IMAC scheme, it is impossible to realize analogue arithmetic multiplication of the same kind of signals and real-time storing the computational results, which limits the application scenarios of IMAC. | |
| "The possible circuits composed of discrete components with operational amplifiers, for performing in-memory analogue arithmetic operations, have been designed in the past based on nonvolatile devices such as memristors," Zhe Guo, a postdoc in Long You’s research group at Huazhong University of Science and Technology, tells Nanowerk. "However, all of the designs so far, have suffered from substantial limitations, including large size, slow response and uneasy on-chip integration." | |
| As the team now reports in Advanced Science ("In-Memory Mathematical Operations with Spin-Orbit Torque Devices"), they introduce spin orbit torque (SOT) devices to experimentally realize in-memory analogue mathematical operations such as summation, subtraction and four-quadrant multiplication, to implement general-purpose applications such as image or signal processing for edge computing. | |
| In addition to nonvolatility and scalability, the CMOS-compatible SOT technique further possesses low energy consumption, high speed and endurance. Therefore, SOT devices offer an avenue for dense in-memory analogue computing paradigms. | |
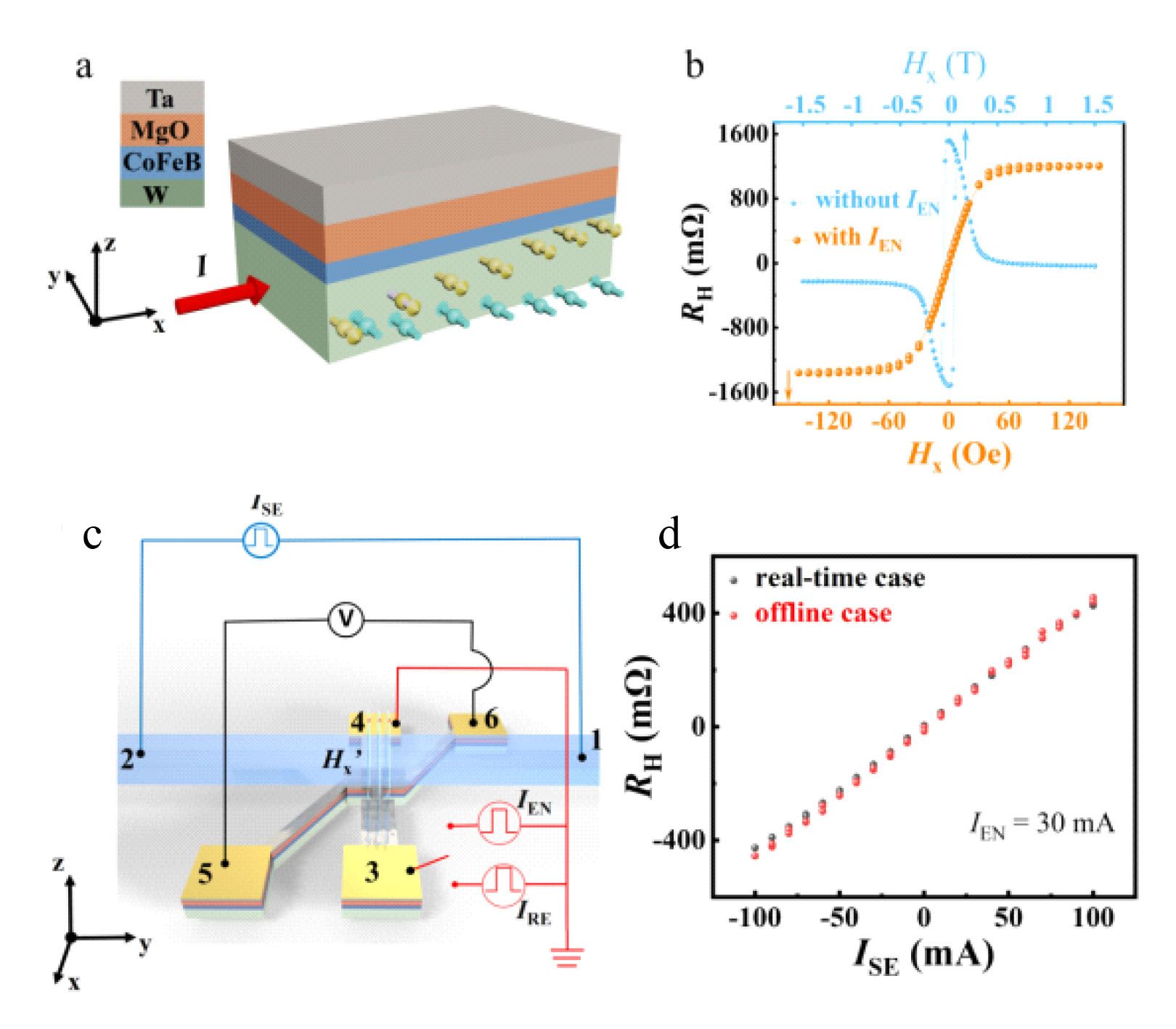 |
|
| Figure 1. Basic in-memory sensing unit. (Image courtesy of the researchers) | |
| As shown in Figure 1 above, the magnetization of heterostructure device (W/CoFeB/MgO/Ta from the bottom, Fig. 1a) with perpendicular magnetic anisotropy can be switched by an in-plane current Ix with the assistance of a collinear magnetic field Hx via SOT. | |
| Moreover, the coercive field of the anomalous Hall effect loop (anomalous Hall resistance RH vs. Hx) decreases with Ix increases. At a specific Ix (named IEN for this Ix), RH varies linearly with applied Hx (Fig. 1b). If there is a current path on the top surface separated by insulating layer (Fig. 1c), a magnetic field along x direction is produced once the electrical current (ISE) flows through the current path. Accordingly, the SOT device is able to sense and memorize the electrical current as RH of the heterostructure (Fig. 1d), via the magnetic field generated by itself. | |
| Particularly, the memory and sensing function can be switched by the IEN signal, namely, the heterostructure can sense the current with the application of IEN while it offline stores ISE at the moment when IEN is switched off. Thus, the device shown in Fig. 1c constitutes the basic in-memory SOT sensing unit. | |
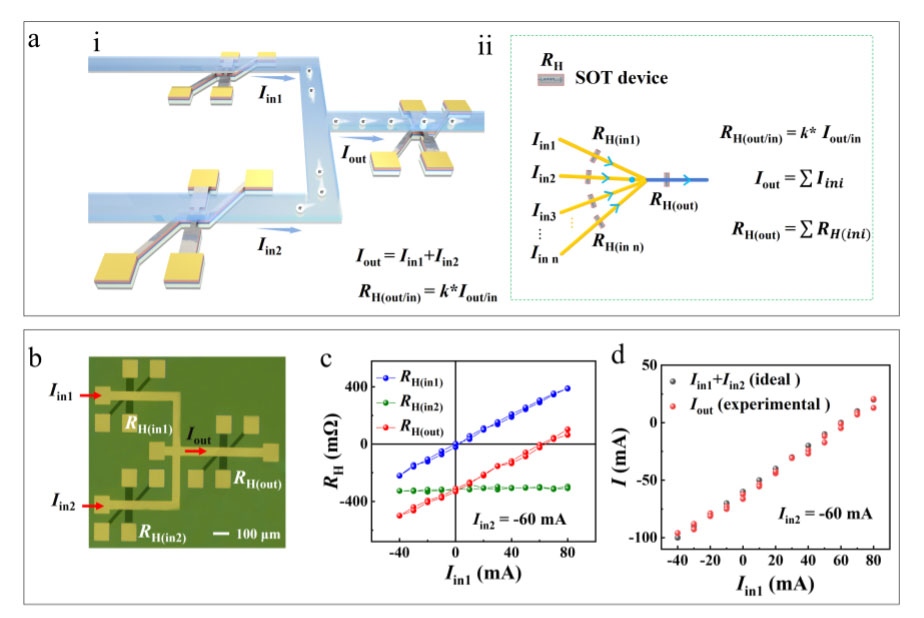 |
|
| Figure 2. In memory analogue summation/subtraction based on interconnected SOT units. (Image courtesy of the researchers) | |
| “Then we can use many SOT units to perform useful functions by building an interconnected network where their sensed current paths are connected to a node,” says Min Song, an Associate Professor at Hubei University, who is also a coauthor of this work. Following this architecture, the electrical currents in the sensed current paths meeting at the common node have to satisfy Kirchhoff’s current law, which clarifies the summation/subtraction correlation of the currents (Fig. 2a). | |
| Correspondingly, the RH of each SOT unit follows the same correlations as the electrical currents. By detecting every individual SOT-device’s RH, one can immediately know every branch current and also their operation relationship. Therefore, in-memory analogue summation/subtraction can be performed in such interconnected SOT-units. | |
| Fig. 2b-d shows the experimental results for three interconnected SOT units. Then the image edge detection is realized based on the adder/subtractor using the Robert operator (Fig. 3a). The left and right panel of Fig. 3b show the original and extracted image, respectively, with a standard deviation of 2.95% in the pixel values. | |
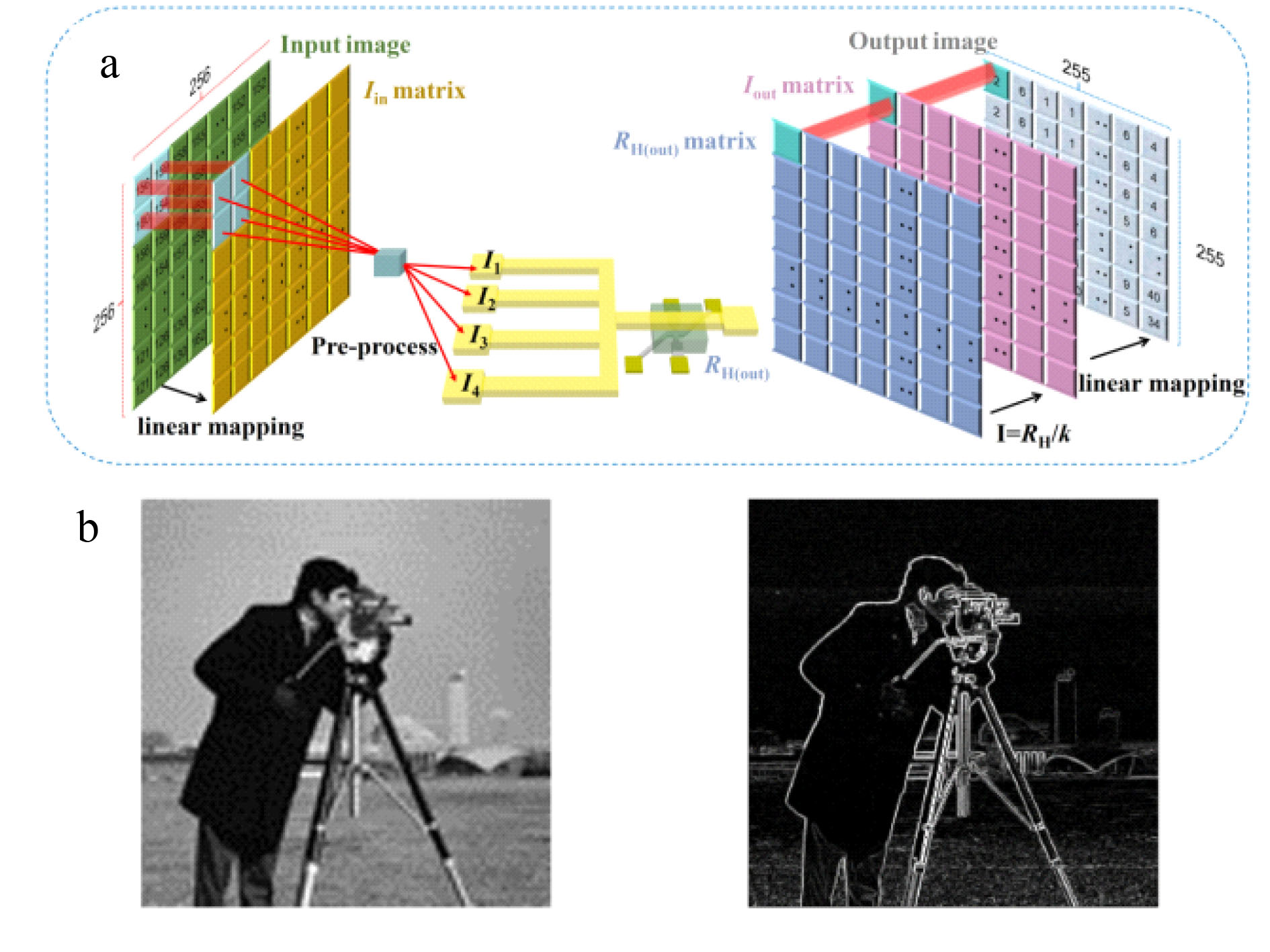 |
|
| Figure 3. Edge detection by the in-memory analogue summation/subtraction computing. (Image courtesy of the researchers) | |
| For a single SOT unit, the anomalous Hall voltage UH is expressed as UH = RH × Ic, where Ic is the current applied along terminals 3 and 4 (Fig. 4a). Additionally, RH can represent the current ISE flowing in the sensed current path, RH = k × ISE. Therefore, UH can be defined as an analogue product of the two current signals ISE and Ic, UH = k × ISE × Ic, if k is a constant and independent of ISE and Ic. Accordingly, in-memory four-quadrant analogue multiplier is realized in a single SOT unit. The amplitude modulation has been implemented based on such a multiplier (Fig. 4d). | |
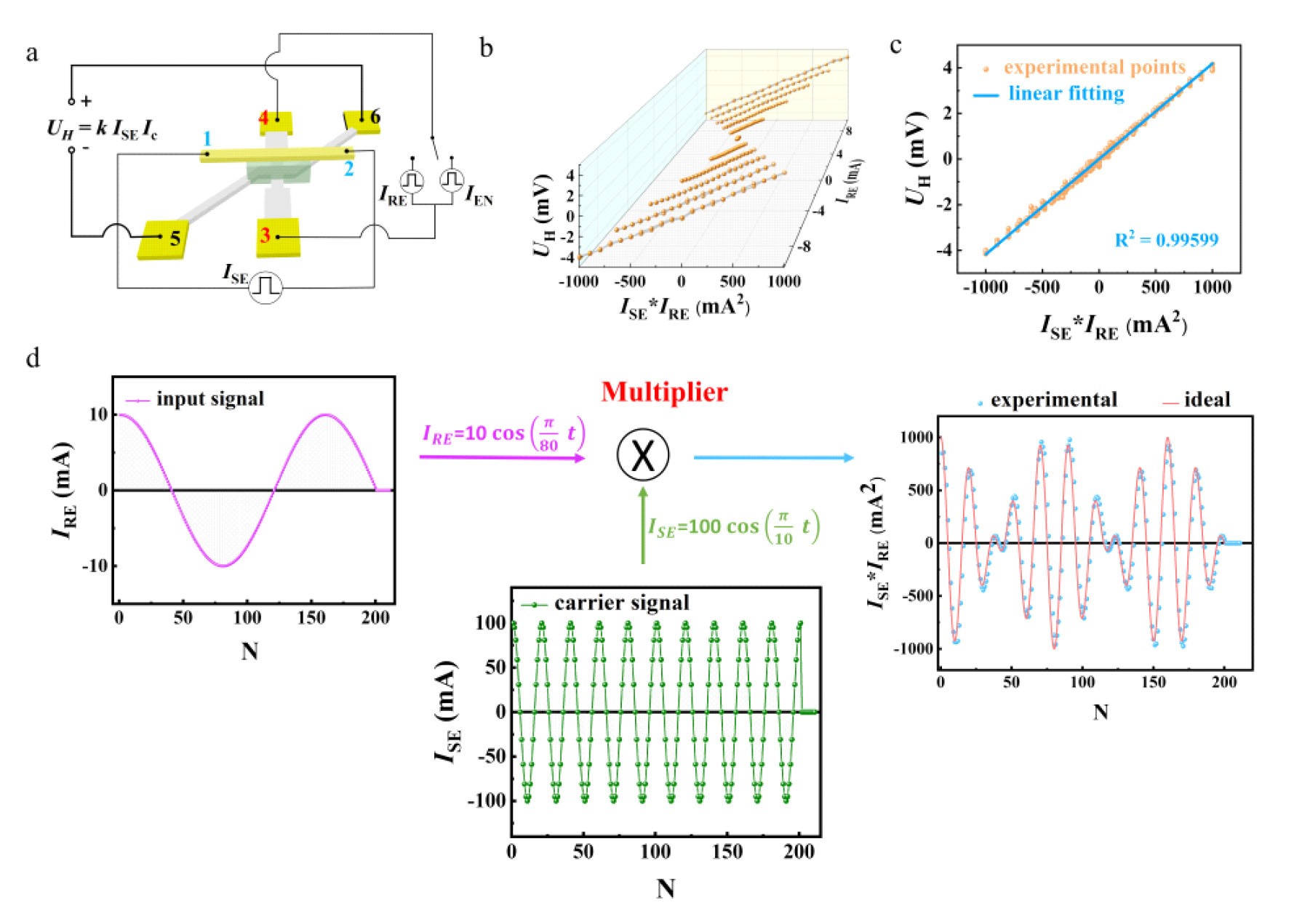 |
|
| Figure 4. In-memory multiplication based on a SOT unit. (Image courtesy of the researchers) | |
| In summary, this work reports a spin-based in-memory analogue computing scheme, which provides an area and energy efficient strategy for on-chip mathematical computation, signal and image processing, and neuromorphic computing. | |
| Provided by Huazhong University of Science and Technology as a Nanowerk exclusive | |
|
Become a Spotlight guest author! Join our large and growing group of guest contributors. Have you just published a scientific paper or have other exciting developments to share with the nanotechnology community? Here is how to publish on nanowerk.com. |
|
