| Posted: Sep 30, 2014 |
At the interface of math and science
|
|
(Nanowerk News) In popular culture, mathematics is often deemed inaccessible or esoteric. Yet in the modern world, it plays an ever more important role in our daily lives and a decisive role in the discovery and development of new ideas — often behind the scenes.
|
|
UC Santa Barbara’s Paul Atzberger, a professor in the Department of Mathematics and in mechanical engineering, often works in areas where science and math intersect. Some of his recent research published in the Proceedings of the National Academy of Science (PNAS) and featured on the cover of the journal Soft Matter focuses on problems specific to lipid bilayer membranes. These microscopic structures can form a sheet that envelopes the outside of a biological cell in much the same way that human skin serves as the body’s barrier to the outside environment.
|
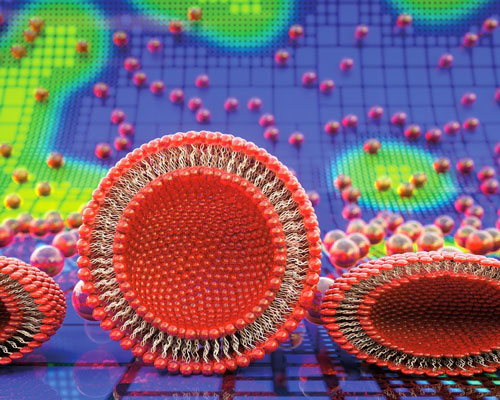 |
| Model of vesicle adhesion, rupture and island dynamics during the formation of a supported lipid bilayer (from work by Atzberger et al) featured on the cover of the journal Soft Matter. (Image: Paul Atzberger)
|
|
In the PNAS paper ("Shape matters in protein mobility within membranes"), Atzberger and his graduate student Jon Karl Sigurdsson worked in collaboration with the experimental laboratory of Patricia Bassereau and David Lacoste at the Institut Curie in Paris, to develop new mathematical approaches to gain insights into how proteins move around within lipid bilayer membranes.
|
|
“Proteins are not just passive voyagers within the bilayer, but rather their very presence can change the local properties of the lipid bilayer membrane in interesting ways,” Atzberger said. “This includes bending the bilayer with a local preferred curvature or changing the nature of a viscous flow. This dual coupling of responding to the local geometry while also affecting it makes it very difficult to formulate concise models and to make predictions.”
|
|
To address these issues, Atzberger developed a statistical mechanics description of the membrane sheet and the proteins based on his past work on immersed-boundary approximations. The idea is to treat the heterogeneous membrane-protein material uniformly but use a moving marker to demarcate the parts associated with the proteins. This approach allows for a simple and reliable description, which captures many of the essential features of membrane-protein dynamics. This not only facilitates performing analytic calculations but also carrying out efficient computational simulations.
|
|
“It used to be just theory and experiment,” Atzberger added. “Now computation serves an ever more important third branch of science. With simulations, one can take underlying assumptions into account in detail and explore their consequences in novel ways. Of course, theory and abstraction are still very important to gain understanding. What computation provides is the ability to grapple with a level of detail and complexity that is often simply beyond the reach of pure theoretical methods.”
|
|
Sophisticated mathematics is often required to bridge the realms of theory, simulation and experiment. Atzberger notes that the order of complexity in biology is especially tricky.
|
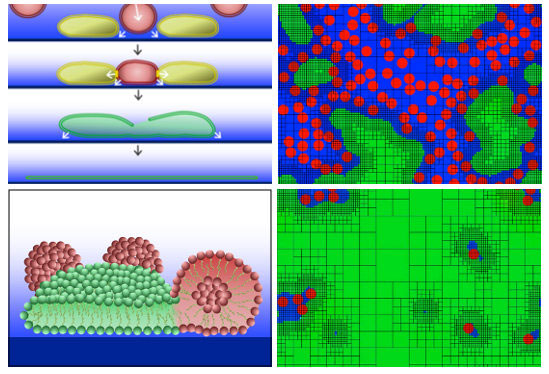 |
| This illustration shows how adhesion forces may drive the merging and rupture events of the vesicles when they are above a critical concentration on the substrate. (Image: Paul Atzberger)
|
|
“If you look at a biological cell, many of our current methods for investigation are similar to looking down from a low-altitude blimp at a big city such as New York or Hong Kong,” he explained. “It’s phenomenally complex, and the level of understanding that can be attained with current methods — while impressive — is also very limited. While experimental methods are advancing, it cannot be ignored that new mathematical approaches are going to be needed for progress.”
|
|
For example, Atzberger’s collaboration with his colleagues in France sought to explore specific mechanisms by which proteins move within bilayers using the idea that the protein locally bends the bilayer and creates a little bump that moves along with the protein.
|
|
“Not only is the protein diffusing but so is that little bump that has to be carried along with it,” Atzberger explained. “This idea has been suggested by a number of theoretical papers. However, in practice this is a really hard thing to measure, particularly because such a mechanism cannot be seen directly since it occurs on length scales that are smaller than the wavelength of visible light. A typical protein is about 10 nanometers in size; the wavelength of visible light is on the order of 300 to 700 nanometers.”
|
|
Because the researchers could not make direct observations, they tagged the protein with quantum dots that emit light when excited. They then tracked and analyzed the motions of individual quantum dots to obtain a measurement of how the individual proteins moved within the bilayer. Like temporarily pulling wrinkles out of a shirt, they applied a tension that would reduce the size and shape of a possible bump induced by a protein. The investigators found that the locally induced shape appears to matter a great deal to a protein’s rate of diffusive motion within the bilayer.
|
|
“This showed us that you cannot ignore the local interactions of the protein that augment the bilayer when considering protein motion,” Atzberger said. “Unlike a particle diffusing in a simple fluid, such complex membrane-protein interactions appear to be at the heart of protein diffusion.
|
|
“These studies are potentially useful, since the rates of protein diffusion play an important role in many cellular processes,” he added. “If you really understand the underlying mechanisms responsible for protein diffusion, you might be able to come up with novel ways to augment it.”
|
|
In related work ("Simulation of edge facilitated adsorption and critical concentration induced rupture of vesicles at a surface") with UCSB colleagues, Atzberger has also applied his mathematical expertise to analyze experiments on supported lipid bilayers (SLB). SLBs are membrane sheets that are bound directly to a surface or anchored in close proximity. They are important in many biophysical studies of membrane-protein interactions and in the development of biosensors.
|
|
Atzberger analyzed experiments conducted by Kim Weirich, then a student in UCSB’s interdepartmental graduate program in biomolecular science and engineering, who investigated an approach in which lipid vesicles are induced to rupture on the substrate to form the SLB. A big challenge is to obtain reliable vesicle rupture and coverage of the substrate.
|
|
To better understand this process, Atzberger and his students developed a mathematical model and computational methods to study the stages in the process of SLB formation. A central question addressed by the model concerns how the SLB process initiates from the crowding of vesicles on the substrate. Another important question is how the lipids from the ruptured vesicles spread out on the substrate as either isolated islands that grow in size or as a multitude of small distinct islands that merge in parallel.
|
|
“Using our computational methods, we were able to simulate rupture events and island dynamics that matched well the trends seen in the experimental data,” Atzberger said. “This led us to strongly favor a specific hypothesis concerning the SLB formulation process: that a local critical concentration of vesicles is required and that the rupture occurs from a mechanism we call ‘adhesive jamming.’
|
|
“By attempting to model the experimental data quantitatively, we found that many of our initial ideas were simply not plausible,” he added. “This led — after a fair amount of thought — to our final model. Of course, more experimental work will be required to see if our theory is ultimately correct. This work was featured on the cover of the journal Soft Matter.
|
|
“I’m proud of these works because we managed to make links between theory, computation and experiment,” Atzberger concluded. “One of my goals as an applied mathematician is to be a bridge between these worlds. When everything comes together harmoniously, this type of research is not only productive but also a lot of fun.”
|


