| Posted: Apr 28, 2015 |
A new constitutive model for the thermo-elasto-plasticity deformation of crystals
|
|
(Nanowerk News) Researchers have proposed a new thermo-elasto-plasticity constitutive model based on the interatomic potential and solid mechanics for metal crystals. Through this new model, the material behavior at different temperatures could be described accurately and conveniently.
|
|
The work, led by Professor Wang TzuChiang, together with collaborators Chen Cen and Tang Qiheng at the State Key Laboratory of Nonlinear Mechanics under the CAS (Chinese Academy of Sciences) Institute of Mechanics, aims to investigate the thermo-elasto-plasticity behavior of metal crystals with a simple and efficient way. A paper describing the team's results is published in the 2015 No.5 issue of SCIENCE CHINA Physics, Mechanics & Astronomy ("A new thermo-elasto-plasticity constitutive equation for crystals").
|
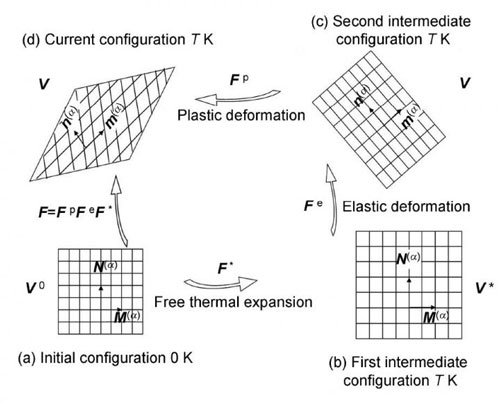 |
| Figure 1: This image shows decomposition of deformation configuration: (a) Initial configuration; (b) first intermediate configuration; (c) second intermediate configuration; (d) current configuration. © Science China Press) (click on image to enlarge)
|
|
In previous researches for metal crystals, some theories based on the quantum mechanics were dependent on the vibration frequencies of lattice and their derivatives, and the calculation process was time-cosuming. On the other hand, for some forthright macroscopic models, the thermal expansion was not considered in the deformation process, and the temperature effects on plastic behavior, such as initial critical resolved shear stress and hardening modulus are difficult to determine. These problems bring inconvenience to prediction of the whole deformation behavior of metal crystals at different temperatures.
|
|
Now, this new research has made an effort to solve these problems and put forward a practical method to obtain the thermo-elasto-plasticity deformation of metal crystals. In this research, the new deformation decomposition is proposed, and the total deformation contains thermal, elastic and plastic parts. The thermal strain can be obtained conveniently by the coefficient of thermal expansion from experimental data. Then, the constitutive equations are established based on the new deformation decomposition. Furthermore, the temperature effects on plastic behavior are reflected by simple expressions, which make the description of the thermo-plasticity behavior more explicitly.
|
|
In this work, to reflect the effect of thermal expansion in the whole deformation process, a new deformation decomposition is given firstly, which is different with kinematical theory for the mechanics of elastic-plastic deformation for crystal. As shown in Figure 1, the deformation configuration is decomposed into four parts: the initial configuration at the undeformed state of 0 K (Figure 1(a)); the first intermediate configuration after free thermal expansions at T K (Figure 1(b)); the second intermediate configuration after elastic deformation at T K (Figure 1(c)); and the current configuration after plastic deformation at T K (Figure 1(d)).
|
|
The new deformation decomposition provides a good basis to establish the constitutive equations and makes the present model applicable to structural calculation with some boundary constraints in the future.
|
|
Then, the increment constitutive equations are obtained at the different deformation stages: the one is established by the rate of the second Piola-Kirchhoff stress and the rate of the Green strain, and the other one is established by the Jaumann rate of the Kirchhoff stress and symmetric parts of the velocity gradient.
|
|
Meanwhile, the temperature dependences of initial critical resolved shear stress and hardening modulus are considered by exponential function. The parameters can be determined easily with three uniaxial stress-strain curves at different temperature. So the plastic behavior at different temperature can be determined accurately.
|
|
Lastly, the stress-strain curves of Al crystals at different temperatures are calculated using this new model, and the calculation results are compared with experimental results. As shown in the Figure 2, the comparisons verify that the new model can predict the thermo-elasto-plasticity behavior of metal crystal very effectively.
|
|
"Comparing with some widely recognized models, this new model has some characteristics as follows: firstly, the new deformation decomposition considers the thermal deformation in the whole deformation process, provides a good basis to establish the constitutive equations and makes the calculation process more simple and explicit than the MD and MC methods. Then the concise expressions for temperature effects on plastic behaviors make this new model have the ability to describe the thermo-elasto-plasticity behavior more clearly and accurately." Said the authors.
|
|
This research provides an applicative method to calculate the thermo-elasto-plasticity deformation at different temperature, which is more explicit and concise than some previous models.
|

