| May 18, 2020 | |
A perfect novel optical vortex with controllable impulse ring profile(Nanowerk News) An optical vortex is identified as a phase singularity encircled with helical wavefront, and thanks to its unique properties including its carried orbital angular momentum (OAM) associated with doughnut-shaped profiles, it has found exciting applications in stimulated emission depletion (STED) nanoscopy, optical manipulation, both quantum and classical OAM-multiplexing optical communications, enhanced optical imaging, and recently in high-intense vortex physics, etc. However, the size of the doughnut-shaped patterns generated by conventional vortices is strongly dependent on the carried topological charge. |
|
| In 2013, Ostrvsky and coworkers first proposed the concept of perfect optical vortices (POVs), which was shaped into an impulse ring at the Fourier plane with its radius being quasi-independent of the topological charge. At the same year, this "perfect" vortex beam was demonstrated for dynamical trapping micro-particles along those bright rings, and it was shown that these perfect vortices provided a possibility to transfer OAM to trapped particles along those bright impulse rings. | |
| One year later, this new type of optical vortices were proposed for OAM-multiplexing optical fiber communications, which provides a possibility to couple multiple OAM beams into a certain annular fiber. However, the impulse rings of those POVs reported in the past are all bright rings, which could also hinder their applications in some scenarios. | |
| Recently, a type of generalized POVs with controllable impulse ring profile based on Circular Dammann Gratings (CDGs) was proposed and demonstrated by a research team from Shanghai Institute of Optics and Fine Mechanics, Chinese Academy of Sciences. The concept was published in Photonics Research ("Circular Dammann gratings for enhanced control of the ring profile of perfect optical vortices"). | |
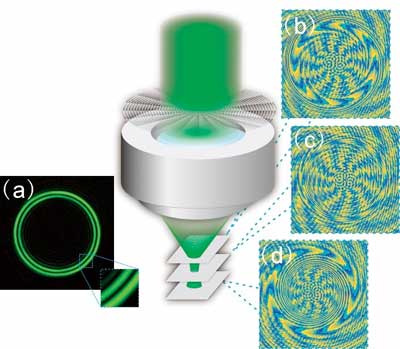 |
|
| The schematic of perfect optical vortices with controllable impulse ring profile. (Image: Shanghai Institute of Optics and Fine Mechanics) | |
| With the development of its design theory, the CDGs had found their applications in optical measurement, optical image encoding, structured light pumping lasers, and annular laser illumination, etc. However, the impulse rings generated by traditional CDGs don't possess any orbital angular momentum. | |
| According to the research group, the Fourier spectrum of each diffraction order of a CDG embedded with a spiral phase was essentially a weight sum of two impulse rings, one inwards- and another outwards-oriented impulse rings. | |
| Thus, it is possible to control the impulse ring profile of the annular ring embedded with spiral phase arbitrarily by changing the weight coefficient between those two impulse rings. | |
| In the proof-of-principle experiment, a programmable spatial light modulator was used to simulate the phase of CDGs embedded with spiral phase, whose structure was optimized to obtain the desired weight coefficient between those two impulse rings. | |
| It showed that a type of "absolute" dark POVs surrounded by two bright lobe-rings in each side was presented, which provided a perfect annular potential well along those dark impulse rings for trapping steadily low-index particles, cells, or quantum gas, etc. | |
| Furthermore, several POVs with different impulse ring profiles, including conventional POVs with bright rings, dark POVs mentioned above, and also POVs with controllable impulse ring profile were demonstrated. | |
| This work opens up new possibilities to arbitrarily reshape the impulse ring profile for perfect vortices. It should be of high interest in optical manipulation, both quantum and classical optical communications, enhanced optical imaging, and also novel structured pumping lasers. |
| Source: Chinese Academy of Sciences | |
|
Subscribe to a free copy of one of our daily Nanowerk Newsletter Email Digests with a compilation of all of the day's news. |
