Topological insulators explained – what they are and what they do

Topological insulators are strange stuff – the bulk of this material is insulating and cannot carry an electrical current, yet the surfaces of the same material are conducting. This means that charged particles can flow freely on their edges and route themselves around defects but can't pass through their interiors.

The electrical properties of these substances result from their topological structure. The almost lossless flow of spin information makes topological insulators’ unique electronic properties make them potentially useful in spintronic devices and even conceivably as transistors for quantum computers.

Topology is a branch of mathematics that describes properties that only change in steps and not continuously - the properties remain intact when an object is stretched, twisted or defor¬med, but not if it is torn apart. Materials properties which stay the same under topological transformations property are known as topological materials.

The concept of topological materials has its roots in the 1970s when (physicists J. Michael Kosterlitz and David J. Thouless used the principles of topology to understand why superconductivity occurs in certain materials only at very low temperatures but disappears at higher temperatures. Later, in the 1980s, F. Duncan M. Haldane used topology to study the properties of chains of small magnets found in some materials.

These three scientists were awarded the Nobel Prize in Physics in 2016 for their groundbreaking work on topological phase transitions and the discovery of topological phases of matter.

Since then, researchers have discovered many materials with special topological properties. These materials can be found not only in thin layers or threads, but also in regular three-dimensional materials. In the past 10 years, this field has become a very important area of research in physics and has generated a lot of excitement because it is believed that topological materials could be used to create new and improved electronics, superconductors, error-tolerant quantum computing, and room temperature spintronics in the future.

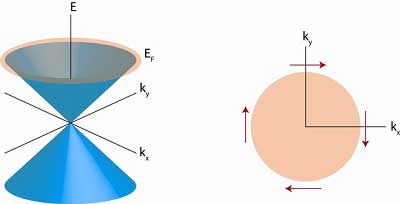
Topological insulators (TIs) are a class of materials with surfaces that host a new quantum state of matter and are insensitive to contaminants, defects and impurities. Surface electrons in TIs behave like massless Dirac particles in a similar way to electrons in graphene. Moreover, surface currents in topological insulators also preserve their spin orientation and coherence on a macro scale.

These inherent properties of TIs, and the interplay between magnetism and proximity to superconductors, make topological insulators a prime platform for the realization of solid-state quantum computing devices

A topological insulator is a material with unique electrical properties resulting from its topological structure. Unlike conventional insulators that have a bulk bandgap that completely blocks the flow of electrical current, topological insulators have a bulk bandgap that is insulating while also having metallic states on their surface.

These surface states are protected by topology – which means that they cannot easily be brought into an insulating state – and are immune to certain types of perturbations, such as impurities and defects, making them robust and ideal for electronic applications. The surface states are characterized by their spin-momentum locking, meaning that the electrons' spin and momentum are correlated in a specific way.

Topological insulators can be classified into different phases, including strong and weak, based on the nature of their surface states. These phases have different properties and are crucial for determining the potential applications of topological insulators.

In 2005, condensed matter physicists Charles Kane and Eugene Mele considered the fate of graphene at low temperatures. Their work ("Quantum Spin Hall Effect in Graphene") would usher in a new era of materials science dealing with topological insulators. In two-dimensions, an ideal topological insulator would have ‘ballistic’ conductance at its edges meaning that electrons traveling through the region would encounter zero resistance (unfortunately though, the 2D topological insulators known to date are disordered and not very easy to work with).

However, the concept of topological insulators was first proposed theoretically already in 1985 and and then in 1987 and later experimentally verified in 2007 in Bi1−x Sbx by Liang Fu and C. L. Kane. (Further investigations confirmed that Bi1−x Sbx is the first realization of a topological insulator in three dimensions and that its surface is a topological metal in two dimensions.

For a detailed discussion on why the surface of Bi1−x Sbx is special that it has these properties read Shou-cheng Zhang’s (excellent viewpoint in Physics Today.

Compounds based on bismuth, antimony, telluride and selenide are the cleanest and most intrinsic topological insulators demonstrated so far and examples (discussed in the literature include Bi2Se3, Bi2Te3, and Sb2Te3.

More recently, researchers have also predicted a new class of topological insulators that have conducting properties on the edges of crystals rather than on their surface, dubbed (higher-order topological insulators.

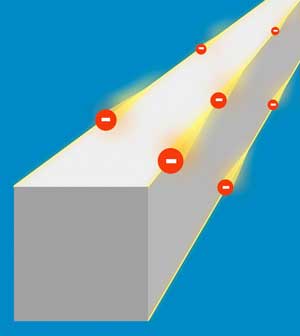
The extraordinary robustness of the conducting edges makes them particularly interesting: The current of topological electrons cannot be stopped by disorder or impurities. If an imperfection gets in the way of the current, it simply flows around the impurity. In addition, the crystal edges do not have to be specially prepared to conduct electrical current. If the crystal breaks, the new edges automatically also conduct current.

One unique property of topological insulators is that the electrons' spin and momentum are correlated in a specific way i.e., they are constrained perpendicular to each other (while this is an essential property of topological insulators, it is not limited to them). This is known as spin-momentum locking, and it makes topological insulators ideal for applications in fields such as spintronics, quantum computing, and thermoelectrics.

Spin-momentum locking is like having a basketball that must rotate in a specific direction depending on its trajectory down the court. Because an electron also carries a magnetic moment, spin-momentum locking can be used to manipulate magnetic systems very efficiently.

Topological insulators offer unique opportunities to control electric currents and magnetism, and are promising materials for future spintronic applications or could provide access to novel, fascinating physical phenomena such as (Majorana fermions or (magnetic monopoles. This is due to their intriguing charge transport channels on their surface, in which the electron spin is coupled to its momentum.

One potential use of topological insulators is as spin filters. Electrons have a quantum property known as spin, which is similar to a magnet with two opposing pole orientations. Conventional electronics ignores electron spin, but the possibility of using spin in electronics, known as spintronics, offers new opportunities for information processing. A spin filter would only allow current to pass if the electrons have the correct spin orientation.

The most promising applications of topological insulators are spintronic devices and dissipationless transistors for quantum computers based on the quantum Hall effect and quantum anomalous Hall effect. In addition, topological insulator materials have also found practical applications in advanced magnetoelectronic and optoelectronic devices.

In the field of quantum computing there is hope that topological qubits could help achieve a breakthrough in the development of a quantum computer designed for universal applications. This type of qubit exhibits the special feature that it is topologically protected; the particular geometric structure of the superconductors as well as their special electronic material properties ensure that quantum information is retained.

Topological qubits are therefore considered to be particularly robust and largely immune to external sources of decoherence. They also appear to enable fast switching times comparable to those achieved by the conventional superconducting qubits used by Google and IBM in current quantum processors.

However, it is not yet clear whether we will ever succeed in actually producing topological qubits. This is because a suitable material basis is still lacking to experimentally generate the special quasiparticles required for this without any doubt. These quasiparticles are also known as Majorana states.

Most topological insulators are also excellent thermoelectric materials, since topological insulator and thermoelectric compounds share similar material features, such as heavy elements and narrow band gaps. While the influence of topological insulator boundary states has long been neglected in early thermoelectric research, a lot of theoretical and experimental investigations have emerged to explore the (contribution of topological insulator boundary states to thermoelectricity.

In addition, the robust metallic states on the surface make TIs ideal for use in electronic devices, where they can be used as interconnects and contacts. See (this review for a broad discussion on topological electronics.

TIs are a revolutionary new class of materials that have unique electronic properties. Their bulk bandgap and robust metallic states on the surface, as well as their spin-momentum locking, make them ideal for a variety of applications, including spintronics, quantum computing, thermoelectrics, and electronic devices. The role of TIs in nanotechnology is also significant, and their unique properties make them potential candidates for use in a variety of nanoscale devices.