| Posted: Dec 18, 2014 |
Revealing the quantum geometry of the graphene lattice
|
|
(Nanowerk News) Among the most revolutionary concepts of modern physics is that the laws of nature are inherently non-local. One striking manifestation of this non-locality was famously predicted by Aharonov and Bohm: a magnetic field confined to the interior of a solenoid can alter the behavior of electrons outside it, shifting the phase of their wave-like interference although they never directly encounter the magnetic field. Originally regarded as a mere curiosity, such “geometric phase shifts” are now known to have dramatic consequences for electron transport in solid-state materials, e.g., allowing unimpeded current flow along the edges of a material that is insulating in the bulk.
|
|
In suitable crystalline structures, geometric phase shifts can arise even in the absence of any magnetic flux, instead induced by an elusive property known as “Berry flux” in momentum space that is difficult to measure directly.
|
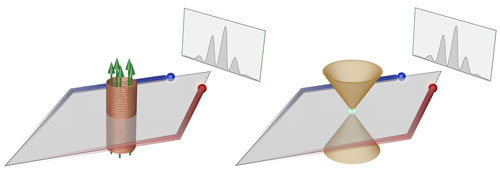 |
| In this new Berry-flux Interferometer with ultracold neutral atoms (right), the Berry curvature of a lattice band structure plays the role of the magnetic field in the original Aharonov-Bohm interferometer (left). Analogous to the original case, the Berry flux enclosed by the interferometer loop gives rise to a measurable phase shift even if the curvature vanishes everywhere along the chosen path.
|
|
Now, scientists at the Ludwig-Maximilians-Universität Munich, the Max Planck Institute of Quantum Optics and Stanford University have demonstrated a matter-wave interferometer that precisely measures Berry flux in an artificial crystal formed by a standing wave of light. Their method, reported this week in Science Express ("An Aharonov-Bohm interferometer for determining Bloch band topology") may ultimately enable new approaches to quantum computation exploiting non-local, topological properties of matter for robust encoding of quantum information.
|
|
In the classic Aharonov-Bohm experiment, a beam of electrons is sent through an interferometer, wherein trajectories passing either left or right of a solenoid converge on a distant screen and form an interference pattern that shifts in proportion to the magnetic flux in the solenoid.
|
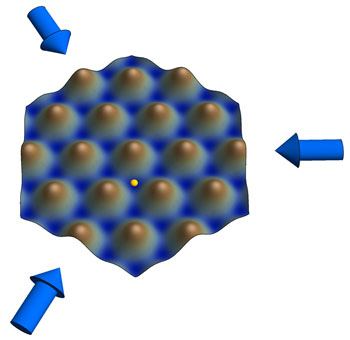 |
| The Graphene-like Honeycomb lattice structure is created by three intersecting laser beams (arrows). The atoms are loaded into the minima (blue) of this potential landscape and can quantum-mechanically tunnel between them. One possible position is illustrated by the small sphere.
|
|
The LMU/MPQ team led by Dr. Ulrich Schneider and Prof. Immanuel Bloch formed an analogous interferometer not with electrons but with neutral atoms, cooled to ultra-low temperature where the wave-like properties of matter are easiest to observe. Lacking electric charge, the atoms experience no geometric phase shift in a true magnetic field and are thus ideally suited to sensing only the surrogate Berry flux. One of the simplest crystalline structures where Berry flux is known to play a role in solid-state physics is the honeycomb lattice of graphene.
|
|
To form a graphene-like lattice potential for ultracold atoms, the researchers use three intersecting laser beams to generate a pattern of light that confines the atoms to a hexagonal grid formed by the intensity minima.
|
|
The most iconic feature in the band structure of graphene is the conical intersection of energy levels known as a Dirac cone, which plays the role of the solenoid in the Berry-flux interferometer. Such conical intersections appear in various contexts ranging from solid-state physics to the energy spectra of molecules and can be shown theoretically to generate a half-quantum of Berry flux—i.e., a geometric phase shift of π in a trajectory that encircles the Dirac cone. Besides having a precisely known value, this flux is expected to be localized to the single point in momentum space where the energy levels intersect, acting as an infinitely narrow solenoid.
|
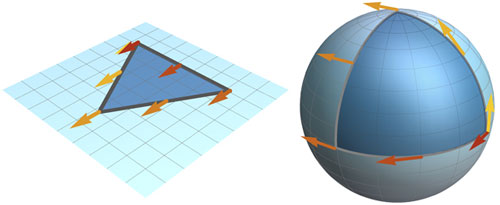 |
| The phase acquired in the Aharonov-Bohm effect is directly analogous to the concept of curvature in geometry. It can be visualized by following a moving vector on a surface. The vector moves such that it remains parallel to the surface and keeps its original angle with the tangent of the path taken (parallel transport).If the surface is flat (left), the vector will remain unchanged while travelling. In contrast, if the surface is curved—such as the surface of a sphere (right) —the vector will rotate while travelling and will not return to its initial direction. Its rotation angle after travelling along a closed loop is a direct measure of the curvature of the surface within the loop. In direct analogy to geometric phases, the rotation angle depends only on the chosen loop and the geometry of the surface, but not on the speed of the movement. Analogously, the state of a quantum system can pick up a geometric phase while completing a closed path in e.g. real space or momentum space, which depends on the enclosed Berry curvature.
|
|
The Dirac cone thus constitutes an ideal test case for the accuracy and resolution of a Berry flux detector. The atom interferometer passes this test with flying colors, revealing precisely the expected phase shift and constraining the location of the responsible flux to a millionth of the lattice’s unit cell in momentum space.
|
|
The interferometric measurement of Berry flux with ultracold atoms is an important milestone in a broad effort to advance control and understanding of the topology of many-particle quantum systems. Driving this effort is the insight that geometric phases can be highly robust to local perturbations that are ordinarily the bane of efforts at storing quantum information.
|
|
In the case of the Aharonov-Bohm interferometer, this robustness is evidenced by the fact that the measured phase is insensitive to the precise position of the solenoid (or the Dirac cone). Only if the localized flux is moved from inside to outside the interferometer arms—altering the topology of the system—does the measured flux suddenly change.
|
|
Realizing visions of topological quantum computation will require significantly more complex topological features that might be engineered by combining effects of geometric phases with control over interparticle interactions. While many challenges still lie ahead, Berry flux interferometry may be celebrated as a new tool for characterizing—and perhaps one day harnessing—topology in ultra-cold atom systems.
|



