| Sep 02, 2015 |
The symmetry of the universe
|
|
(Nanowerk News) Our existence is still a great mystery in theoretical physics. Why did anti-matter disappear almost completely from our universe, whereas matter did not? Scientists are attempting to solve this mystery at the particle accelerator of the major European research institute at CERN.
|
|
The ALICE collaboration has now published the most precise measurement of the properties of light atomic nuclei and anti-nuclei ever made in Nature Physics ("Precision measurement of the mass difference between light nuclei and anti-nuclei").
|
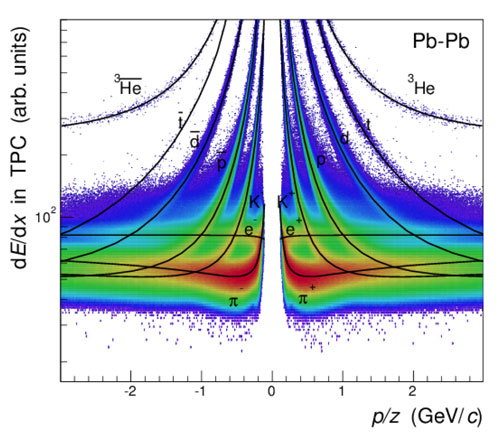 |
| Measurements of energy loss in the time-projection chamber enable the ALICE experiment to identify antinuclei (upper curves on the left) and nuclei (upper curves on the right) produced in the lead-ion collisions at the LHC. (Image: CERN)
|
|
Scientists from the Technical University of Munich (TUM) are working on new detectors for the ALICE experiment which will allow measurements with even greater precision in the future.
|
|
What did the universe look like shortly after it came into being? The ALICE experiment (A Large Ion Collider Experiment) at CERN in Switzerland concerns itself with this question. At the largest particle accelerator in the world, the Large Hadron Collider (LHC), researchers let lead nuclei and protons collide at the highest beam energies to date. The temperatures thereby created are 100,000 times higher than those in the center of the Sun.
|
|
"A state is created that is very similar to the one after the Big Bang," explains Laura Fabbietti, Professor in the Physics Department. She and Dr. Torsten Dahms head the two experimental ALICE groups at the TU Munich.
|
|
This state of matter, the so-called quark-gluon-plasma (QGP), probably formed one microsecond after the Big Bang, a point in time when the universe was expanding at great speed. The QGP produced in the laboratory is stable only for 10-23 seconds, but, during this very short time, the researchers have the opportunity to look back into the past of the universe.
|
|
Matter-antimatter asymmetrie remains a mystery
|
|
Furthermore, the ALICE experiment makes it possible to get to the bottom of one of mankind’s biggest mysteries. According to the CPT theorem (charge, parity, time), there is a fundamental symmetry between particles and antiparticles in our Universe. Specifically, there should be no difference between our Universe and one where all particles are exchanged with antiparticles (and vice versa), if the Universe is also inverted in time and space.
|
|
There has to be a difference nevertheless, because the theory says that equal quantities of matter and antimatter should have been produced during the Big Bang. When particles and antiparticles meet, they annihilate each another. However, nowadays we almost only observe particles - there must therefore have been an imbalance.
|
|
Most accurate measurements to date
|
|
Physicists are looking for a violation of the CPT theorem which would help to explain the existing matter-antimatter asymmetry. "ALICE is attempting to find a difference by means of high-precision measurements of the properties of particles and their antiparticles which are produced in particle collisions at the LHC," explains Dahms. In the current study, the researchers investigated the mass-to-charge ratio of helium-3 nuclei and deuterium nuclei and their respective antiparticles. Charge and mass are determined by measuring the particle traces and the particle’s specific energy loss within a gas detector called the TPC. The TCP is thus the heart of the ALICE detector system. The results published in "Nature Physics" are the most accurate measurements to date in this field and at the moment confirm the CPT theorem.
|
|
The researchers are currently working on improvements to the ALICE detectors with the aim of making the investigations even more precise. "At the moment we are able to record 500 collisions per second," explains Fabbietti. "Soon it should be 50,000 collisions per second." The TUM groups are working on an upgrade of the TPC read out, which is to become much faster. The existing multi-wire chambers are being replaced by state of the art GEM foils that provide better spatial resolution as well. The TUM group heads the GEM-TPC upgrade project for ALICE as part of an international collaboration. The installation of the new detectors is planned for 2018.
|

