Logo

Moebius rings enable new ways to control light in twisted spaces
(Nanowerk Spotlight) The field of topological photonics has witnessed remarkable progress over the past decade, providing a robust platform for studying light-matter interactions and enabling the development of novel optical devices. However, the ability to control and modulate topological phase transitions has remained a significant challenge, particularly in non-Euclidean systems.
Non-Euclidean systems refer to geometrical spaces that do not adhere to the familiar rules of Euclidean geometry, which is based on flat planes and straight lines. Instead, these systems can involve curved surfaces or spaces where parallel lines may converge or diverge, introducing complexity and richness in behavior that are not present in flat, Euclidean spaces. This divergence from the Euclidean framework presents unique challenges and opportunities for manipulating light in ways that are not possible in conventional optical systems.
Now, a team of researchers from Peking University and Beijing Institute of Technology has made a groundbreaking discovery by demonstrating spin-controlled topological phase transitions in non-Euclidean optical systems using innovative Möbius ring configurations.
They reported their findings in Frontiers of Optoelectronics ("Spin‑controlled topological phase transition in non‑Euclidean space").
Topological photonics has its roots in the study of topological insulators, materials that exhibit unique electronic properties due to their topology. These materials have an insulating interior but conduct electricity on their surface, leading to robust and protected edge states. Researchers have sought to translate these principles to the realm of photonics, aiming to create optical systems with similar topological properties.
While significant progress has been made in realizing topological photonic systems in Euclidean geometries, such as photonic crystals and metamaterials, the exploration of non-Euclidean topological photonics has remained largely uncharted territory.
The key challenge in non-Euclidean topological photonics lies in the complex interplay between the system's geometry and its topological properties. Conventional optical components, such as waveguides and resonators, are typically designed in Euclidean space, where the curvature is zero.
However, non-Euclidean geometries, characterized by non-zero curvature, introduce additional complexity and richness to the system's behavior. The Möbius strip, a surface with only one side and one boundary, is a prime example of a non-Euclidean geometry that has captured the imagination of scientists and mathematicians alike.
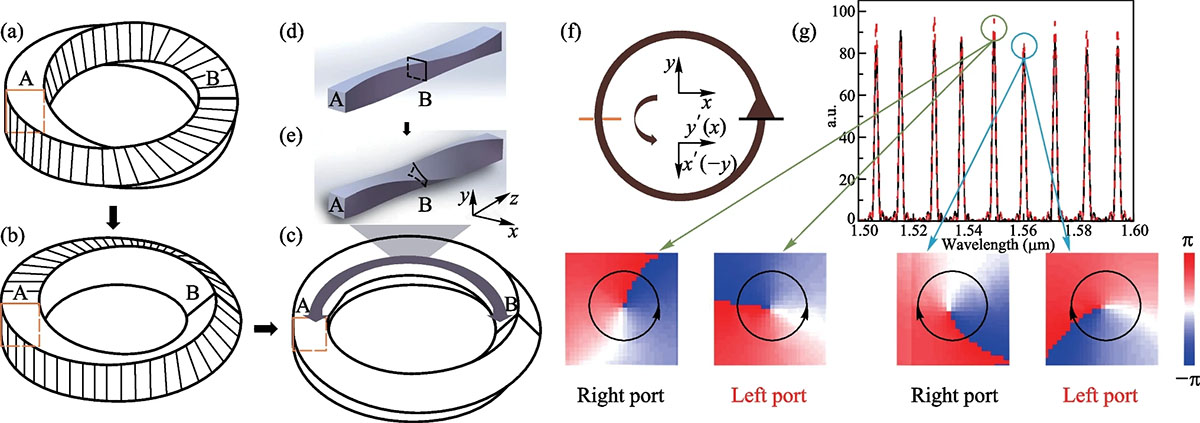
In their groundbreaking work, the research team, led by Professors Xiaoyong Hu and Qihuang Gong, has harnessed the unique properties of the Möbius strip to demonstrate spin-controlled topological phase transitions in non-Euclidean optical systems. The key innovation lies in the design of a novel Möbius ring configuration with an 8π period and a π/2 twist. This configuration exploits the spin-locked effect, where the transverse electric and transverse magnetic modes of the waveguide are interconverted as light propagates along the Möbius ring.
Design of 8π period Möbius ring
a A regular Möbius ring with 4π period. b 8π period Möbius ring. c 8π period Möbius ring with length/width adiabatic evolution. d Length/width adiabatic evolution in straight waveguide. e Length/width adiabatic evolution in straight waveguide with twist operation. f Light travel through one turn in the 8π period Möbius ring. g Transmittance spectra for 8π period Möbius ring of right port (black line) and left port (dotted red line), as well as the phase distribution along the propagation direction. Transmittance spectra means the ratio of the electric field intensity that can be transmitted through the port to the incident electric field intensity, and its changing with the wavelength. (Image: Frontiers of Optoelectronics, CC BY) (click on image to enlarge)
To understand the significance of the spin-locked effect, consider a simple analogy. Imagine a figure skater spinning on ice. Just as the skater's spin direction can be controlled by changing the orientation of their arms, the spin-locked effect allows scientists to control the behavior of light by manipulating its orientation within the Möbius ring. This enables a new degree of control over light propagation in these twisted spaces.
The researchers utilized these 8π period Möbius rings to construct both one-dimensional Su-Schrieffer-Heeger (SSH) and two-dimensional coupled resonator optical waveguide (CROW) configurations. These configurations exhibit a remarkable property: they support topological edge states excited by circularly polarized light of a specific handedness, while forbidding the excitation of topological modes by light of the opposite handedness. This spin-dependent behavior opens up new possibilities for controlling and manipulating topological states in optical systems.
The team further demonstrated that the transition from topological edge states to bulk states can be conveniently achieved by controlling the circular polarization of the incident light. This spin-controlled topological phase transition was observed in both Hermitian and non-Hermitian cases, highlighting the robustness and versatility of the approach. The non-Hermitian case, where gain and loss are introduced into the system, adds an additional layer of complexity and richness to the topological behavior.
The implications of this work are far-reaching. By leveraging the spin-locked effect in non-Euclidean Möbius ring configurations, researchers can now explore a new dimension in topological photonics. The ability to control topological phase transitions using the spin of light opens up exciting possibilities for designing robust optical devices and studying fundamental aspects of light-matter interactions in non-Euclidean geometries.
For instance, this discovery could pave the way for more secure and reliable optical communication systems. By encoding information in the topological edge states within Möbius rings, data could be transmitted with greater resilience against disturbances and errors. This could revolutionize industries such as telecommunications, enhancing the speed and reliability of data transmission.
Furthermore, the ability to control light in non-Euclidean geometries could inspire new designs for optical sensors and imaging devices. By exploiting the unique properties of Möbius rings, researchers could develop sensors with improved sensitivity and resolution, enabling breakthroughs in fields such as biomedical imaging, environmental monitoring, and materials science.
The work by Hu, Gong, and their colleagues represents a significant step forward in the field of topological photonics. By bridging the gap between non-Euclidean geometries and topological physics, they have opened up a new frontier in the study of light-matter interactions. The ability to control topological phase transitions using the spin of light not only deepens our understanding of fundamental physical principles but also paves the way for the development of novel optical devices with enhanced functionality and robustness.
As the field of topological photonics continues to evolve, the incorporation of non-Euclidean geometries and spin-controlled phase transitions is expected to play an increasingly important role. The work by Hu, Gong, and their team serves as a beacon, guiding researchers towards unexplored territories and inspiring new avenues of investigation. The marriage of topology and geometry in photonics promises to unlock a wealth of scientific discoveries and technological advancements in the years to come.
The demonstration of spin-controlled topological phase transitions in non-Euclidean optical systems marks a significant milestone in the quest to harness the power of topology for light manipulation and control. As researchers continue to push the boundaries of what is possible in topological photonics, the work by Hu, Gong, and their colleagues will undoubtedly serve as a foundation for future explorations and innovations in this exciting field.
Michael Berger By – Michael is author of three books by the Royal Society of Chemistry:
Nano-Society: Pushing the Boundaries of Technology,
Nanotechnology: The Future is Tiny, and
Nanoengineering: The Skills and Tools Making Technology Invisible
Copyright © Nanowerk LLC
 

Become a Spotlight guest author! Join our large and growing group of guest contributors. Have you just published a scientific paper or have other exciting developments to share with the nanotechnology community? Here is how to publish on nanowerk.com.