| Posted: Apr 02, 2015 |
Two-dimensional dirac materials: Structure, properties, and rarity
|
|
(Nanowerk News) Graphene, a two-dimensional (2D) honeycomb sheet composed of carbon atoms, has attracted intense interests worldwide because of its outstanding properties and promising prospects in both basic and applied science. The great development of graphene is closely related to the unique electronic structure, that is, Dirac cones. The cone which represents linear energy dispersion at Fermi level gives graphene massless fermions, leading to various quantum Hall effects, ultra high carrier mobility, and many other novel phenomena and properties.
|
|
Dirac cone is special but might not unique to graphene. Recently, more and more 2D materials have been predicted to possess Dirac cones, such as silicene and germanene (graphene-like silicon and germanium, respectively), several graphynes (sp-sp2 carbon allotropes), and so on. But these 2D Dirac systems are so rare compared to the numerous 2D materials. A deep understanding of all known 2D Dirac systems and a strategy to seek for new ones are needed.
|
|
A new paper published in National Science Review presented the recent progress on theoretical studies of various 2D Dirac materials ("The rare two-dimensional materials with Dirac cones").
|
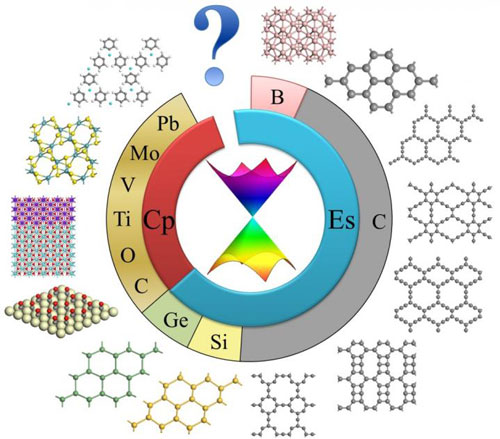 |
| This is a scheme of 2-D materials with Dirac cones. (©Science China Press)
|
|
In this paper, the structural and electronic properties of graphene, silicene, germanene, graphynes, several boron and carbon allotropes, transition metal oxides, organic and organometallic crystals, square MoS2, and artificial lattices (electron gases and ultracold atoms) were summarized. As the author stated, "most Dirac materials have spatial inversion symmetry", "Many of them are bipartite and composed of only one element", and "hexagonal honeycomb structure is common in atomic Dirac materials". Since "the Dirac-cone structure gives graphene massless fermions, leading to half-integer/fractional/fractal quantum Hall effects, ultrahigh carrier mobility", other 2D Dirac systems were predicted to have similar properties, and some even possess new physics beyond graphene.
|
|
Based on the above discussions, the authors further investigated how Dirac points move and merge in these systems. They mentioned that strain can move the Dirac point to a new k (reciprocal) location. But "when two Dirac points with opposite Berry phases move in the k space under any perturbation and arrive at the same point, they merge and their Berry phases annihilate each other". Moreover, the von Neumann-Wigner theorem was applied to explain the scarcity of 2D Dirac systems. Then rigorous requirements for a 2D system to achieve Dirac cones were deduced, which is related to the symmetry, parameters, Fermi level, and band overlap.
|
|
This paper noted that "Dirac cones are not only the linear energy dispersion around discrete points but also singularities in the spectrum of Hamiltonians and are topologically protected." The authors pointed out "Looking forward, we believe that more and more 2D Dirac materials will be discovered, and a thorough understanding on the existing conditions of Dirac cones is greatly helpful in seeking/designing new systems."
|

